Burkholder-Davis-Gundy inequality
Consider a regular martingale  ,
, 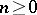 ,
,  almost surely. Let
almost surely. Let 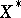 and
and 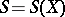 stand for
stand for 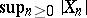 and the quadratic variation
and the quadratic variation  , respectively.
, respectively.
The following inequality in  -spaces was proved in [a2]:
-spaces was proved in [a2]:
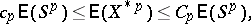 | (a1) |
where 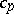 and
and 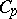 are positive constants depending only on
are positive constants depending only on 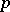 ,
, 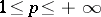 .
.
In fact, this inequality was proved in three steps; D.L. Burkholder [a3] proved the cases  ; Burkholder and R.F. Gundy [a4] proved the cases
; Burkholder and R.F. Gundy [a4] proved the cases 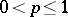 for a large class of martingales, and Gundy [a5] proved the case
for a large class of martingales, and Gundy [a5] proved the case 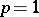 for all martingales.
for all martingales.
Moreover, (a1) was proved in a more general form in Orlicz spaces (cf. Orlicz space) in [a2]:
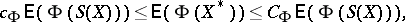 | (a2) |
where 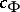 and
and 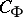 are positive constants depending only on
are positive constants depending only on 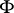 .
.
The inequalities (a1) and (a2) are frequently used in martingale theory, harmonic analysis and Fourier analysis (cf. also Fourier series; Fourier transform).
For a different proof of these inequalities, see, e.g., [a1].
References
| [a1] | N.L. Bassily, "A new proof of the right hand side of the Burkholder–Davis–Gundy inequality" , Proc. 5th Pannonian Symp. Math. Statistics, Visegrad, Hungary (1985) pp. 7–21 |
| [a2] | D.L. Burkholder, B. Davis, R.F. Gundy, "Integral inequalities for convex functions of operators on martingales" , Proc. 6th Berkeley Symp. Math. Statistics and Probability , 2 (1972) pp. 223–240 |
| [a3] | D.L. Burkholder, "Martingale transforms" Ann. Math. Stat. , 37 (1966) pp. 1494–1504 |
| [a4] | D.L. Burkholder, R.F. Gundy, "Extrapolation and interpolation for convex functions of operators on martingales" Acta Math. , 124 (1970) pp. 249–304 |
| [a5] | B. Davis, "On the integrability of the martingale square function" Israel J. Math. , 8 (1970) pp. 187–190 |
Burkholder-Davis-Gundy inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Burkholder-Davis-Gundy_inequality&oldid=14650