Convex integration

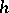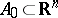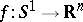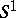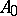One of the methods developed by M. Gromov to prove the -principle. The essence of this method is contained in the following statement: If the convex hull of some path-connected subset contains a small neighbourhood of the origin, then there exists a mapping whose derivative sends into . This is equivalent to saying that the differential relation for mappings 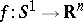given by requiring 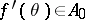for all 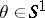satisfies the 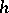-principle. More generally, the method of convex integration allows one to prove the 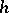-principle for so-called ample relations 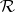. In the simplest case of a 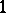-jet bundle 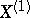over a 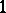-dimensional manifold 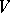, this means that the convex hull of 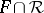is all of 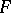for any fibre 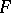of 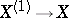(notice that this fibre is an affine space). The extension to arbitrary dimension and higher-order jet bundles is achieved by studying codimension-one hyperplane fields in 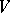and intermediate affine bundles 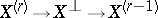defined in terms of .

One particular application of convex integration is to the construction of divergence-free vector fields and related geometric problems.

References

[a1]	M. Gromov, "Partial differential relations" , Ergebn. Math. Grenzgeb. (3) , 9 , Springer (1986) MR0864505 Zbl 0651.53001
[a2]	D. Spring, "Convex integration theory" , Monogr. Math. , 92 , Birkhäuser (1998) MR1488424 Zbl 0997.57500