Reduced scheme
From Encyclopedia of Mathematics
A scheme whose local ring at any point does not contain non-zero nilpotent elements. For any scheme 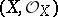 there is a largest closed reduced subscheme
there is a largest closed reduced subscheme 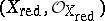 , characterized by the relations
, characterized by the relations
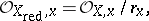 |
where 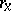 is the ideal of all nilpotent elements of the ring
is the ideal of all nilpotent elements of the ring 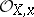 . A group scheme over a field of characteristic 0 is reduced [3].
. A group scheme over a field of characteristic 0 is reduced [3].
References
| [1] | M. Artin, "Algebraic approximation of structures over complete local rings" Publ. Math. IHES , 36 (1969) pp. 23–58 MR0268188 Zbl 0181.48802 |
| [2] | A. Grothendieck, J. Dieudonné, "Eléments de géométrie algebrique I. Le langage des schémas" Publ. Math. IHES , 4 (1960) MR0217083 MR0163908 Zbl 0118.36206 |
| [3] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701 |
Comments
That a group scheme over a field of characteristic  is reduced is called Cartier's theorem, cf. also [a1].
is reduced is called Cartier's theorem, cf. also [a1].
It may happen that a scheme 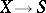 over a base scheme
over a base scheme 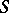 is reduced but that
is reduced but that  is not reduced (even with
is not reduced (even with 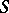 and
and 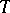 reduced). The classical objects of study in algebraic geometry are the algebraic schemes which are reduced and which stay reduced after extending the base field.
reduced). The classical objects of study in algebraic geometry are the algebraic schemes which are reduced and which stay reduced after extending the base field.
References
| [a1] | F. Oort, "Algebraic group schemes in characteristic zero are reduced" Invent. Math. , 2 (1969) pp. 79–80 MR0206005 Zbl 0173.49002 |
| [a2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
How to Cite This Entry:
Reduced scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reduced_scheme&oldid=14264
Reduced scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reduced_scheme&oldid=14264
This article was adapted from an original article by S.G. Tankeev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article