Solv manifold

solvmanifold, solvable manifold

A homogeneous space 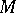of a connected solvable Lie group 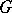(cf. Lie group, solvable). It can be identified with the coset space 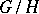, where 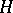is the stabilizer subgroup of some point of the manifold .

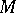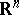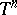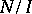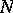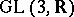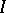Examples: , the torus , the Iwasawa manifold (where is the group of all upper-triangular matrices with 1's on the main diagonal in and is the subgroup of all integer points in 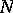), 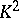(the Klein bottle), and 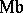(the Möbius band).

The first solvmanifolds studied were those in the narrower class of nil manifolds (cf. Nil manifold), that is, homogeneous spaces of nilpotent Lie groups (such as 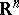, , 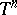, 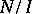but not 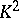and 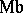). The following results are due to A.I. Mal'tsev (see [5]). 1) Every nil manifold is diffeomorphic to 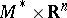, where 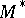is a compact nil manifold. 2) If 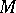is compact and 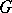acts effectively on 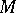, then the stabilizer is a discrete subgroup. 3) A nilpotent Lie group 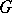(cf. Lie group, nilpotent) acts transitively and locally effectively on some compact manifold if and only if its Lie algebr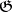a has a 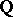-form. If, in addition, 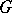is simply connected, then it is isomorphic to a unipotent algebraic group defined over 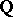and 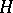is an arithmetic subgroup of 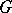. 4) The fundamental group 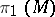of a compact nil manifold 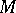(which is isomorphic to 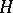when 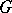is simply connected and its action on 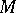is locally effective) determines it up to a diffeomorphism. The groups that can arise here are just the finitely-generated nilpotent torsion-free groups.

These results admit partial generalizations to arbitrary solvmanifolds. Thus, for any solvmanifold 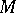there is a solvmanifold 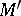which is a finitely-sheeted covering of it and is diffeomorphic to 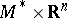, where 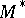is some compact solvmanifold. An arbitrary solvmanifold cannot always be decomposed into a direct product 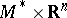, but it is diffeomorphic (see [1], [4]) to the space of a vector bundle over some compact solvmanifold (for 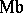the corresponding bundle is a non-trivial line bundle over ). The fundamental group 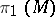of an arbitrary solvmanifold 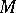is polycyclic (cf. Polycyclic group), and if 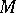is compact, it determines 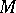uniquely up to a diffeomorphism. A group 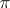is isomorphic to 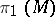for some compact solvmanifold 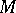if and only if it is contained in an exact sequence of the form

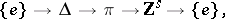where 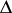is a finitely-generated nilpotent torsion-free group. Every polycyclic group has a subgroup of finite index that is isomorphic to 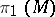for some compact solvmanifold . If a solvable Lie group 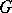acts transitively and locally effectively on a compact solvmanifold 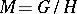, then is fibred over a torus with fibre 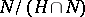, where 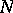is the nil radical of 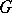. A solvmanifold 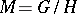is compact if and only if there is a 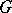-invariant measure on 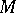with respect to which the volume of 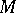is finite.

Every solvmanifold 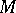is aspherical (that is, the homotopy group 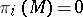for 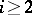). Among all compact homogeneous spaces, compact solvmanifolds are characterized by asphericity and the solvability of 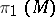(see [3]).

References

[1]	L. Auslander, "An exposition of the structure of solvmanifolds I, II" Bull. Amer. Math. Soc. , 79 : 2 (1973) pp. 227–261; 262–285 MR486308
[2]	L. Auslander, R. Szczarba, "Vector bundles over tori and noncompact solvmanifolds" Amer. J. Math. , 97 : 1 (1975) pp. 260–281 MR0383443 Zbl 0303.22006
[3]	V.V. Gorbatsevich, "On Lie groups, transitive on Solv manifolds" Math. USSR.-Izv. , 11 (1977) pp. 271–291 Izv. Akad. Nauk. SSSR Ser. Mat. , 41 (1977) pp. 285–307
[4]	G. Mostow, "Some applications of representative functions to solvmanifolds" Amer. J. Math. , 93 : 1 (1971) pp. 11–32 MR0283819 Zbl 0228.22015
[5]	M. Raghunatan, "Discrete subgroups of Lie groups" , Springer (1972)