Brunn-Minkowski theorem

Let 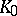and be convex sets in an -dimensional Euclidean space; let 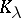, , 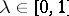be the set of points which divide segments with end points at any points of the sets 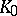and 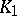in the ratio 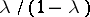(a linear combination of 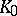and 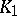); and let be the -th power root of the volume of the set 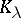. Then 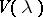is a concave function of , i.e. the inequality

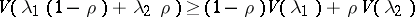is valid for all . The function 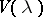is linear (and the inequality then becomes an equality) if and only if 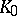and 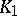are homothetic. The Brunn–Minkowski theorem can be generalized to linear combinations of several convex sets. It is used to solve extremal and uniqueness problems. It was discovered by H. Brunn in 1887, and completed and rendered more precise in 1897 by H. Minkowski.

References

[1]	H. Busemann, "Convex surfaces" , Interscience (1958)
[2]	H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957)

References

[a1]	K. Leichtweiss, "Konvexe Mengen" , Springer (1979)