Hahn decomposition
From Encyclopedia of Mathematics
Revision as of 18:03, 26 April 2012 by Boris Tsirelson (talk | contribs) (→References: Royden: internal link)
A partition of a set 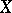 , on which a
, on which a  -additive set function
-additive set function  is given on the
is given on the  -algebra
-algebra  of subsets, into two subsets
of subsets, into two subsets  and
and 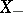 ,
, 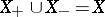 , such that
, such that 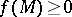 if
if 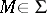 ,
, 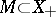 , and
, and 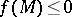 if
if 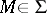 ,
,  . Such a partition of
. Such a partition of  is not unique, in general.
is not unique, in general.
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
Comments
See also Jordan decomposition. Instead of Hahn decomposition the phrase Hahn–Jordan decomposition is also used.
References
| [a1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [a2] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 57 |
| [a3] | H.L. Royden, "Real analysis", Macmillan (1968) |
How to Cite This Entry:
Hahn decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hahn_decomposition&oldid=13726
Hahn decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hahn_decomposition&oldid=13726
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article