Unitary group
relative to a form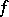 
The group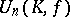 
of all linear transformations 
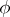of an 
-dimensional right linear space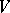 
over a skew-field 
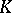, preserving a fixed non-singular sesquilinear (relative to an involuti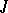on 
on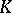 
) form 
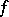on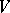 
, i.e. a 
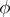such that
 |
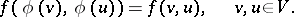A unitary group is a classical group. Particular cases of unitary groups are a symplectic group (in this case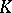 
is a field, 
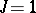and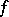 
is an alternating bilinear form) and an orthogonal group (
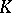is a field, 
, 
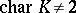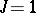and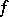 
is a symmetric bilinear form). Henceforth, suppose that 
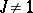and that 
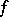possesses property 
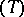(cf. Witt theorem). Multiplying 
by a suitable scalar, one can, without changing the unitary group, arrange that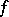 
is a Hermitian form, and moreover, by changing 
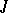, that 
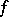is skew-Hermitian.
If one excludes the case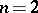 
, 
, then every element of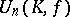 
can be written as a product of at most 
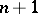pseudo-reflections (i.e. transformations fixing all elements of some non-isotropic hyperplane in 
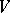). The centre 
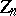of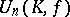 
consists of all homotheties of 
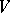of the form 
, 
, 
.
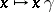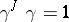Let 
be the Witt index of the form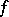 
. If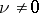 
, it will be convenient to take 
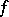skew-Hermitian. Let 
be the normal subgroup of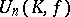 
generated by the unitary transvections, i.e. by the linear transformations of the form 
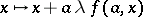, where 
is an isotropic vector in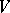 
and 
. The centre of the group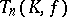 
is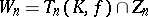 
. The quotient group 
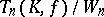is simple for 
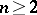, provided 
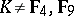. The structure of the quotient group 
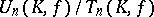may be described as follows. Let 
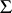be the subgroup of the multiplicative group 
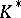of 
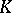generated by 
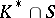and let 
be the subgroup of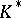 
generated by the elements 
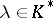with the following property: In 
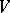there exists a hyperbolic plane (i.e. a non-isotropic two-dimensional subspace containing an isotropic vector) such that 
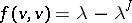for a certain vector 
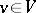orthogonal to the given plane. This subgroup is normal in 
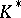. Let 
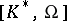be the subgroup of 
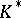generated by the commutators 
, 
, 
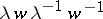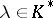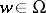. If one excludes the case 
, 
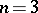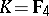, then 
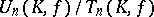is isomorphic to 
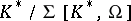for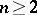 
.
In many cases the group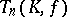 
coincides with the commutator subgroup of 
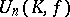; this is true, for example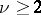, if 
. If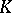 
is commutative and 
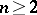, then 
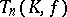coincides with the normal subgroup 
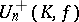of all elements with Dieudonné determinant (cf. Determinant) equal to 1 (excluding the case 
, 
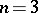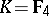). The relation between 
and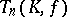 
has also been studied in the case when the skew-field 
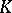is finite dimensional over its centre [1].
Suppose now that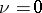 
. Then many of the stated results no longer hold (there are examples of unitary groups having an infinite series of normal subgroups with Abelian factors, examples of unitary groups for which 
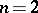and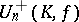 
does not coincide with the commutator subgroup, etc.). The case most studied is that of locally compact skew-fields of characteristic 
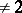and algebraic number fields.
One of the basic results on automorphisms of unitary groups is the following (cf. [1]): If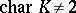 
and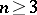 
, then every automorphism of the unitary group 
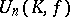has the form 
, 
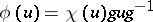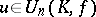, where 
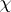is a homomorphism of 
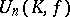into its centre 
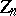and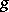 
a unitary semi-similitude of 
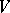(i.e. a bijective semi-linear mapping 
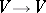satisfying the condition 
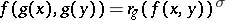, where 
, 
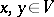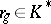and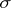 
is the automorphism of 
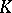associated with 
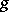). If 
is even,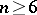 
, 
is a field of characteristic 
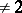and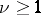 
, then every automorphism of 
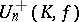is induced by an automorphism of 
.
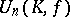If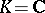 
, 
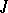is the automorphism of complex conjugation and the Hermitian form 
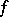is positive definite, then the unitary group 
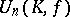is denoted by 
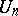; it is a real compact connected Lie group and is often simply called the unitary group. In the case of an indefinite form 
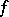the group 
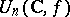is often called pseudo-unitary. By the choice of a basis in 
, 
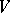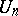may be identified with the group of all unitary matrices (cf. Unitary matrix). In that case the group 
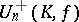is called the special unitary group and is denoted by 
.
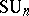References
Unitary group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_group&oldid=13710