Dini-Lipschitz criterion
From Encyclopedia of Mathematics
Revision as of 18:51, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Dini–Lipschitz criterion to Dini-Lipschitz criterion: ascii title)
If a continuous 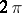 -periodic function
-periodic function 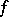 satisfies the condition
satisfies the condition
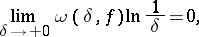 |
where 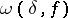 is the modulus of continuity of the function
is the modulus of continuity of the function 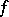 , then its Fourier series converges uniformly to it on the entire real axis. The criterion was demonstrated by U. Dini [1], and also by R. Lipschitz for the special case when
, then its Fourier series converges uniformly to it on the entire real axis. The criterion was demonstrated by U. Dini [1], and also by R. Lipschitz for the special case when 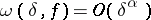 ,
, 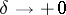 , for any
, for any 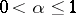 [2]. The Dini–Lipschitz criterion is a final (sharp) statement in the following sense. If
[2]. The Dini–Lipschitz criterion is a final (sharp) statement in the following sense. If  is an arbitrary modulus of continuity satisfying the condition
is an arbitrary modulus of continuity satisfying the condition
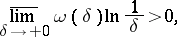 |
then there exists a continuous 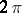 -periodic function
-periodic function 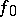 whose Fourier series diverges at some point, while
whose Fourier series diverges at some point, while 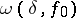 satisfies the condition
satisfies the condition 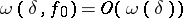 .
.
References
| [1] | U. Dini, "Sopra la serie di Fourier" , Pisa (1872) |
| [2] | R. Lipschitz, "De explicatione per series trigonometricas instituenda functionum unius variabilis arbitrariarum, etc." J. Reine Angew. Math. , 63 : 2 (1864) pp. 296–308 |
| [3] | H. Lebesgue, "Sur la répresentation trigonométrique approchée des fonctions satisfiasants à une condition de Lipschitz" Bull. Soc. Math. France , 38 (1910) pp. 184–210 |
| [4] | S.M. Nikol'skii, "On the Dini–Lipschitz condition for convergence of Fourier series" Doklady Akad. Nauk SSSR , 73 : 3 (1950) pp. 457–460 (In Russian) |
| [5] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
How to Cite This Entry:
Dini-Lipschitz criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dini-Lipschitz_criterion&oldid=13476
Dini-Lipschitz criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dini-Lipschitz_criterion&oldid=13476
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article