Turbulent system

surging system

A dynamical system with a state space containing turbulence manifolds, i.e. manifolds, the crossing of which alters the law governing the motion of the system. A turbulent system in 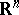is described by several systems of differential equations

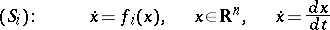and by surfaces

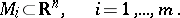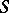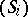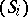When a trajectory of in the region meets the surface , a turbulence occurs, i.e. the system is replaced by 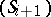, while 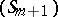coincides with 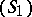(for more details see [3]). The participation of several differential systems 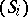in the definition of a turbulent system results in a large diversity of phase portraits of such systems. For instance, the turbulent system described by two stationary systems of linear differential equations

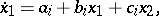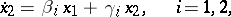having the straight line as turbulence manifolds 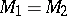may, in particular, have a limit cycle [3], [4]. Turbulent systems supply specific models of non-linear vibrations, thus permitting one to describe "hysteresis" phenomena.

References

[1]	T. Vogel, "Sur les systèmes déferlants" Bull. Soc. Math. France , 81 (1953) pp. 63–75 MR0058053 Zbl 0051.08301
[2]	T. Vogel, "Systèmes déferlants, systèmes héréditaires, systèmes dynamiques" , Qualitative Methods in Nonlinear Vibration Theory (Proc. Internat. Symp. Nonlinear Vibrations 1961) , 2 , Kiev (1963) pp. 123–130 MR0159451 Zbl 0152.28801
[3]	A.D. Myshkis, A.Ya. Khokhryakov, "Surging dynamical systems I. Singular points in the plane" Mat. Sb. , 45 (87) : 3 (1958) pp. 401–414 (In Russian) Zbl 0081.30702
[4]	J.I. Gil'derman, "On the limit cycles of piecewise affine systems" Soviet Math. Dokl. , 17 : 5 (1976) pp. 1328–1332 Dokl. Akad. Nauk SSSR , 230 : 3 (1976) pp. 512–515 Zbl 0382.34016

Comments

The phrase "turbulent system" has not been used in the English language literature for this notion. (Actually, the above-described system does not have a specific name attached to it, except in [1]–[3].)

For turbulence of fluids see Turbulence, mathematical problems in.

Analogous notions occur in control theory and statistics. In control theory one considers control systems whose dynamics are given by different (differential) equations in different regimes of state space, often as an approximation of a non-linear control system by different linearizations in different parts of state space. The phase "sliding controlsliding control" and "control schedulingcontrol scheduling" are sometimes used to refer to control laws in such settings.

In both statistics and control theory one considers random processes which are governed by a number of possible laws and sudden transitions from one law to another can take place. The problem in statistics of detecting that such a change-over has taken place is known as change-point detection.