Cauchy Schwarz inequality

The Cauchy inequality for finite sums of real numbers is the inequality

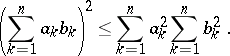Proved by A.L. Cauchy (1821); the analogue for integrals is known as the Bunyakovskii inequality.

The Cauchy inequality is also the name used for an inequality for the modulus of a derivative of a regular analytic function at a fixed point of the complex plane , or for the modulus of the coefficients of the power series expansion of ,

These inequalities are

(*)

where is the radius of any disc 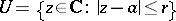on which 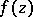is regular, and is the maximum modulus of 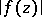on the circle . The inequalities (*) occur in the work of A.L. Cauchy (see e.g. ). They directly imply the Cauchy–Hadamard inequality (see ):

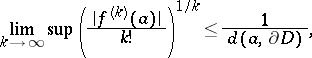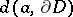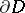where is the distance from to the boundary of the domain of holomorphy of . In particular, if is an entire function, then at any point ,

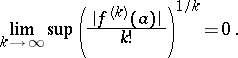For a holomorphic function 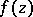of several complex variables 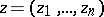, , 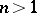the Cauchy inequalities are

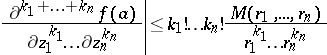or

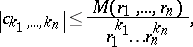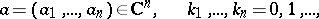where are the coefficients of the power series expansion of :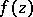

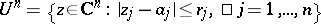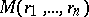are the radii of a polydisc on which is holomorphic, and is the maximum of 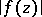on the distinguished boundary of .

For references see Cauchy–Hadamard theorem.

Comments

In Western literature the name Bunyakovskii inequality is rarely used. Both the inequality for finite sums of real numbers, or its generalization to complex numbers (see Bunyakovskii inequality), and its analogue for integrals are often called the Schwarz inequality or the Cauchy–Schwarz inequality.

The distinguished boundary of a polydisc 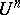as above is the set .