Gâteaux gradient
From Encyclopedia of Mathematics
Revision as of 18:52, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Gâteaux gradient to Gateaux gradient: ascii title)
of a functional 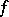 at a point
at a point 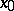 of a Hilbert space
of a Hilbert space 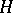
The vector in 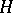 equal to the Gâteaux derivative
equal to the Gâteaux derivative 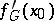 of
of 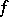 at
at 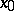 . In other words, the Gâteaux gradient is defined by the formula
. In other words, the Gâteaux gradient is defined by the formula
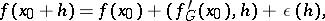 |
where 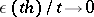 as
as 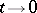 . In an
. In an  -dimensional Euclidean space the Gâteaux gradient
-dimensional Euclidean space the Gâteaux gradient 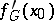 is the vector with coordinates
is the vector with coordinates
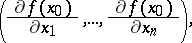 |
and is simply known as the gradient. The concept of the Gâteaux gradient may be extended to the case when 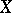 is a Riemannian manifold (finite-dimensional) or an infinite-dimensional Hilbert manifold and
is a Riemannian manifold (finite-dimensional) or an infinite-dimensional Hilbert manifold and 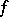 is a smooth real function on
is a smooth real function on 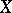 . The growth of
. The growth of 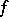 in the direction of its Gâteaux gradient is larger than in any other direction passing through the point
in the direction of its Gâteaux gradient is larger than in any other direction passing through the point 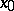 .
.
How to Cite This Entry:
Gâteaux gradient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A2teaux_gradient&oldid=12952
Gâteaux gradient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A2teaux_gradient&oldid=12952
This article was adapted from an original article by V.M. Tikhomirov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article