Cartan-Weyl basis

of a finite-dimensional semi-simple complex Lie algebra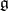

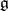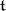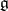A basis of consisting of elements of a Cartan subalgebra of and root vectors 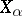, , 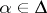where 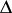is the system of all non-zero roots of 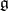with respect to 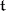. The choice of a Cartan–Weyl basis is not unique. A root 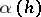, , 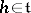is identified, as a linear form on 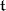, with the vector 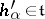such that 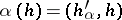, where 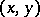is the Killing form in 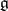. Here

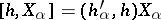for each 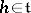. If 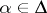, then 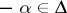and the root vectors 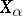can be chosen such that 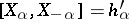. If 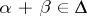, then

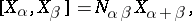where 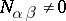. If 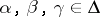, , 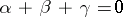then 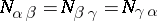. There exists a normalization of the vectors 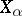for which 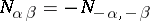, where the numbers 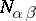obtained are rational. There exists a normalization of the vectors 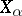under which all 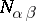are integers (see Chevalley group). The definition of a Cartan–Weyl basis (introduced by H. Weyl in [1]), as well as everything mentioned above concerning the vectors 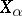, 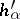and the numbers 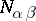, carry over verbatim to the case of an arbitrary finite-dimensional split semi-simple Lie algebra over a field of characteristic zero and its root decomposition with respect to a split Cartan subalgebra.

References

[1]	H. Weyl, "Theorie der Darstellung kontinuierlicher halb-einfacher Gruppen durch lineare Transformationen I" Math. Z. , 23 (1925) pp. 271–309
[2]	N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979))
[3]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)

Comments

See also Lie algebra, semi-simple for a description of the special case of a Chevalley basis.

References

[a1]	J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966)
[a2]	J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4
[a3]	R.W. Carter, "Simple groups of Lie type" , Wiley (Interscience) (1972)