Stable rank

Let 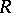be an associative ring with unit element. A sequence of elements 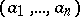is called left unimodular if the left ideal generated by the 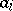, , 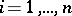is all of .

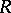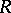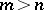The left stable rank of is the least integer such that for each and left unimodular sequence 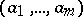there are 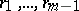such that 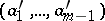with 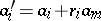, , 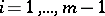is also left unimodular.

The right stable rank of 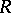is defined analogously by replacing left with right everywhere. The left and right stable ranks are equal [a1], cf. also, e.g., [a2], §11.3, and both are therefore called the stable rank of 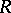, denoted by .

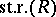By writing a left unimodular sequence 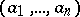as a column, there is a natural left action of on 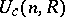, the set of all left unimodular sequences of length . The general linear rank, 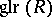, of 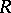is the least integer such that 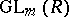acts transitively on for all 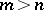. This is equivalent to the property that all right stably-free modules of rank 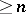are free, [a2].

Recall that 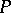is stably free if 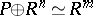for some 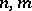; the rank of 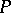is then defined as 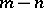. This is well-defined if 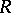has the invariant basis property (i.e. 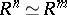if and only if 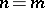). This property holds, e.g., if 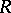is commutative or right Noetherian.

One has 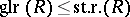, so that any stably-free module of rank 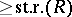is free.

For a field 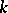one has 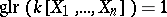for all .

Let 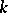be a field of transcendence degree 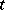over its prime subfield 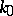. The Kronecker dimension of 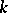is then defined as 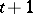if 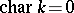and as 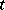otherwise. For 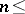Kronecker dimension o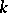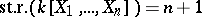f , . If 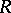is commutative of Krull dimension (cf. also Dimension of an associative ring), then 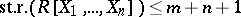(Bass' theorem).

Let 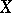be a topological space, 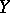a metric space and 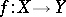a continuous mapping. A point 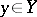is a stable value of if it is in 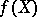and if there is an such that for every continuous mapping 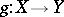with 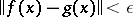for all 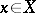it is still true that 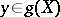. The mapping dimension of a topological space 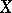, , 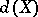is the largest integer 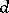for which there exists a mapping 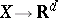for which the origin is a stable value. (If no such 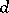exists, 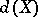is set equal to 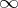.) For nice spaces, e.g., metrizable, separable, , this concept of dimension coincides with other notions of dimension, such as inductive dimension, [a5], Chapt. VI, §1 (cf. Dimension theory). It always coincides with the notion of dimension defined by essential mappings (cf. Dimension theory), [a5], Chapt. VI, §3.

Let 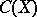be the ring of real-valued continuous functions on a topological space and 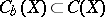the subring of bounded functions. Then 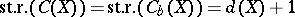(Vaserstein's theorem).

Both Bass' and Vaserstein's theorem indicate that 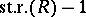is a good dimension concept for rings.

More generally, the stable rank is defined for subrings and ideals of an associative ring 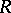with unit.

Let 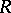be an associative ring with unit, and let 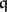be a subring (possibly without unit) of 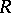. A sequence of elements 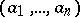is left 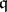-unimodular if it is left unimodular (in 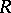) and, moreover, 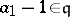, , 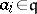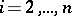. The stable rank of the subring 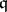is the least number such that for each left 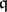-unimodular sequence of length 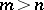there are 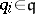, , 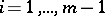such that 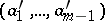, with 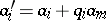, is a left 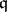-unimodular sequence of length 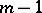. (Such a property is referred to as a stable range condition, cf., e.g., [a4]). The stable rank of 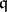does not depend on the ambient ring 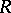. Again it is true that the notion of stable rank is left/right symmetric, [a1].

References

[a1]	L.N. Vaserstein, "Stable ranks of rings and dimensionality of topological spaces" Funct. Anal. Appl. , 5 (1971) pp. 102–110 Funkts. Anal. i Prilozhen. , 5 : 2 (1970) pp. 17–27
[a2]	J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) MR934572
[a3]	A.J. Hahn, O.T. O'Meara, "The classical groups and 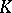-theory" , Springer (1981) pp. §4.1 MR1007302 MR0842441
[a4]	H. Bass, "Algebraic 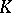-theory" , Benjamin (1968) pp. Chapt. V, §3 MR249491
[a5]	W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948)