Second fundamental form

of a surface

The quadratic form in the differentials of the coordinates on the surface which characterizes the local structure of the surface in a neighbourhood of an ordinary point. Let the surface be given by the equation

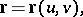where and are internal coordinates on the surface; let

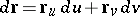be the differential of the position vector along a chosen direction of displacement from a point to a point (see Fig.). Let

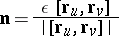be the unit normal vector to the surface at the point 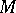(here 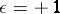if the vector triplet has right orientation, and in the opposite case). The double principal linear part 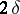of the deviation of the point on the surface from the tangent plane at the point is

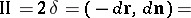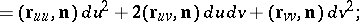it is known as the second fundamental form of the surface.

Figure: s083700a

The coefficients of the second fundamental form are usually denoted by

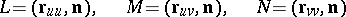or, in tensor notation,

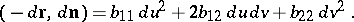The tensor is called the second fundamental tensor of the surface.

See Fundamental forms of a surface for the connection between the second fundamental form and other surface forms.

References

[a1]	W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) MR0350630 Zbl 0264.53001