Support of a measure
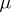
The set 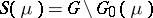 , where
, where 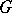 is a locally compact Hausdorff space on which the regular Borel measure
is a locally compact Hausdorff space on which the regular Borel measure  is given and
is given and 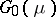 is the largest open set for which
is the largest open set for which  . In other words,
. In other words, 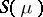 is the smallest closed set on which
is the smallest closed set on which  is concentrated. (Here,
is concentrated. (Here,  is concentrated on
is concentrated on  if
if 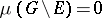 .) If
.) If  is compact, then
is compact, then 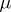 is called of compact support.
is called of compact support.
Comments
The support of a measure 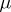 on a topological space
on a topological space 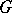 can be defined whenever the union of all
can be defined whenever the union of all 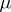 -zero open subsets is still of measure zero. This is the case if
-zero open subsets is still of measure zero. This is the case if 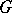 has a countable base, or if
has a countable base, or if 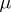 is tight or Radon (see Regular measure), but it is not always the case if
is tight or Radon (see Regular measure), but it is not always the case if 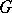 is only locally compact and
is only locally compact and 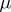 is not tight.
is not tight.
Of course, one can always define, for a measure 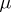 on a topological space
on a topological space 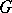 with topology
with topology  ,
,
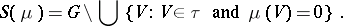 |
But then it is not necessarily true that 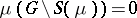 , contradicting the intuitive idea of a support.
, contradicting the intuitive idea of a support.
References
| [a1] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 57 MR0210528 Zbl 0142.01701 |
| [a2] | H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 MR0257325 Zbl 0176.00801 |
Support of a measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Support_of_a_measure&oldid=12419