Namespaces
Variants
Actions

Difference between revisions of "Symmetrization (of tensors)"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48929 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
One of the operations in tensor algebra that constructs a symmetric tensor (relative to a group of indices) from a given tensor. Symmetrization always takes place over several upper or lower indices. A tensor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917501.png" /> with components <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917502.png" /> is the result of symmetrization of a tensor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917503.png" /> with components <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917504.png" /> relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917505.png" /> upper indices, for example relative to the group of indices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917506.png" />, if
−
s0917501.png
 
−
$#A+1 = 22 n = 0
 
−
$#C+1 = 22 : ~/encyclopedia/old_files/data/S091/S.0901750 Symmetrization (of tensors)
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
  
−
{{TEX|auto}}
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917507.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table>
−
{{TEX|done}}
 
  
−
One of the operations in tensor algebra that constructs a symmetric tensor (relative to a group of indices) from a given tensor. Symmetrization always takes place over several upper or lower indices. A tensor  $  S $
+
Here the summation is taken over all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917508.png" /> permutations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s0917509.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175010.png" />. Symmetrization relative to a group of lower indices is defined similarly. Symmetrization with respect to a group of indices is defined by placing these indices between round brackets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175011.png" />. The fixed indices (those not used in the symmetrization) are distinguished by vertical lines. For example (symmetrization over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175012.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175013.png" /> remains fixed),
−
with components  $  \{ s _ {j _ {i}  \dots j _ {q} } ^ {i _ {1} \dots i _ {p} } :  1 \leq  i _  \nu  , j _  \mu  \leq  n \} $
 
−
is the result of symmetrization of a tensor  $  T $
 
−
with components  $  \{ t _ {j _ {1}  \dots j _ {q} } ^ {i _ {1} \dots i _ {p} } : 1 \leq  i _  \nu  , j _  \mu  \leq  n \} $
 
−
relative to  $  m $
 
−
upper indices, for example relative to the group of indices  $  I = ( i _ {1} \dots i _ {m} ) $,  
 
−
if
 
  
−
$$ \tag{* }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175014.png" /></td> </tr></table>
−
s _ {j _ {1}  \dots j _ {q} } ^ {i _ {1} \dots i _ {p} }  = \
 
−
{
 
−
\frac{1}{m!}
 
−
}
 
−
\sum _ {I \rightarrow \alpha }
 
−
t _ {j _ {1}  \dots j _ {q} } ^ {\alpha _ {1} \dots \alpha _ {m} i _ {m + 1 }  \dots i _ {p} } .
 
−
$$
 
  
−
Here the summation is taken over all  $  m! $
+
Successive symmetrization relative to groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175017.png" />, coincides with symmetrization relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175018.png" />. In other words, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175019.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175020.png" /> (inner brackets are removed).
−
permutations  $  \alpha = ( \alpha _ {1} \dots \alpha _ {m} ) $
 
−
of  $  I $.  
 
−
Symmetrization relative to a group of lower indices is defined similarly. Symmetrization with respect to a group of indices is defined by placing these indices between round brackets  $  (  ) $.  
 
−
The fixed indices (those not used in the symmetrization) are distinguished by vertical lines. For example (symmetrization over  $  4, 1, 7 $;
 
−
$  5 $
 
−
remains fixed),
 
−
 
 
−
$$
 
−
t ^ {( 4 | 5 | 17) }  = \
 
−
{
 
−
\frac{1}{3!}
 
−
}
 
−
[ t  ^ {4517} + t  ^ {1574} +
 
−
t  ^ {7541} + t  ^ {4571} +
 
−
t  ^ {7514} + t  ^ {1547} ].
 
−
$$
 
−
 
 
−
Successive symmetrization relative to groups  $  I _ {1} $
 
−
and  $  I _ {2} $,
 
−
$  I _ {1} \subset  I _ {2} $,  
 
−
coincides with symmetrization relative to $  I _ {2} $.  
 
−
In other words, if $  s _ {j _ {1}  \dots j _ {q} } = t _ {( j _ {1}  \dots ( j _ {k} \dots j _ {1} ) \dots j _ {q} ) } $,  
 
−
then $  s _ {j _ {1}  \dots j _ {q} } = t _ {( j _ {1}  \dots j _ {q} ) } $(
 
−
inner brackets are removed).
 
  
 
A tensor which does not change on symmetrization with respect to some group of indices is called a [[Symmetric tensor|symmetric tensor]].
 
A tensor which does not change on symmetrization with respect to some group of indices is called a [[Symmetric tensor|symmetric tensor]].
Line 60: Line 15:
 
The multiplication of two or more tensors, followed by symmetrization of the product relative to all indices, is called symmetric multiplication. Symmetrization of tensors, side by side with the alternation operation, is used for the decomposition of a tensor into tensors with a simpler structure. Symmetrization is also used for the formation of sums of the form (*) with multi-indexed terms. For example, if the elements of the matrix
 
The multiplication of two or more tensors, followed by symmetrization of the product relative to all indices, is called symmetric multiplication. Symmetrization of tensors, side by side with the alternation operation, is used for the decomposition of a tensor into tensors with a simpler structure. Symmetrization is also used for the formation of sums of the form (*) with multi-indexed terms. For example, if the elements of the matrix
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175021.png" /></td> </tr></table>
−
\left \|
 
  
 
commute under multiplication, then the expression
 
commute under multiplication, then the expression
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091750/s09175022.png" /></td> </tr></table>
−
n!  a _ {1}  ^ {(} 1 a _ {2}  ^ {2} \dots a _ {n}  ^ {n)}  = n! \
 
−
a _ {(} 1  ^ {1} a _ {2}  ^ {2} \dots a _ {n)}  ^ {n}  = n! \
 
−
a _ {(} 1  ^ {(} 1 a _ {2}  ^ {2} \dots a _ {n)}  ^ {n)}
 
−
$$
 
  
 
is called the permanent of the matrix.
 
is called the permanent of the matrix.
Line 75: Line 25:
 
====References====
 
====References====
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  P.A. Shirokov,  "Tensor calculus. Tensor algebra" , Kazan'  (1961)  (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  D.V. Beklemishev,  "A course of analytical geometry and linear algebra" , Moscow  (1971)  (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  J.A. Schouten,  "Tensor analysis for physicists" , Cambridge Univ. Press  (1951)</TD></TR></table>
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  P.A. Shirokov,  "Tensor calculus. Tensor algebra" , Kazan'  (1961)  (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  D.V. Beklemishev,  "A course of analytical geometry and linear algebra" , Moscow  (1971)  (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top">  J.A. Schouten,  "Tensor analysis for physicists" , Cambridge Univ. Press  (1951)</TD></TR></table>
 +
 +
  
 
====Comments====
 
====Comments====

Revision as of 14:53, 7 June 2020

One of the operations in tensor algebra that constructs a symmetric tensor (relative to a group of indices) from a given tensor. Symmetrization always takes place over several upper or lower indices. A tensor with components is the result of symmetrization of a tensor with components relative to upper indices, for example relative to the group of indices , if

(*)

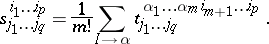Here the summation is taken over all permutations of . Symmetrization relative to a group of lower indices is defined similarly. Symmetrization with respect to a group of indices is defined by placing these indices between round brackets . The fixed indices (those not used in the symmetrization) are distinguished by vertical lines. For example (symmetrization over 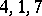; remains fixed),

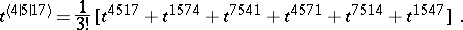Successive symmetrization relative to groups 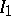and 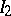, , 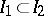coincides with symmetrization relative to . In other words, if , then (inner brackets are removed).

A tensor which does not change on symmetrization with respect to some group of indices is called a symmetric tensor.

Symmetrization, with respect to some group, of a tensor which was alternated first (see Alternation) with respect to that group, leads to the zero tensor.

The multiplication of two or more tensors, followed by symmetrization of the product relative to all indices, is called symmetric multiplication. Symmetrization of tensors, side by side with the alternation operation, is used for the decomposition of a tensor into tensors with a simpler structure. Symmetrization is also used for the formation of sums of the form (*) with multi-indexed terms. For example, if the elements of the matrix

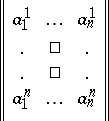commute under multiplication, then the expression

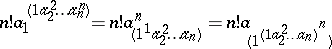is called the permanent of the matrix.

References

[1] P.A. Shirokov, "Tensor calculus. Tensor algebra" , Kazan' (1961) (In Russian)
[2] D.V. Beklemishev, "A course of analytical geometry and linear algebra" , Moscow (1971) (In Russian)
[3] J.A. Schouten, "Tensor analysis for physicists" , Cambridge Univ. Press (1951)


Comments

Cf. also the editorial comments to Symmetrization.

References

[a1] M.A. Akivis, V.V. Goldberg, "An introduction to linear algebra & tensors" , Dover, reprint (1977) (Translated from Russian)
[a2] M. Marcus, "Finite dimensional multilinear algebra" , 1 , M. Dekker (1973) pp. 77ff
How to Cite This Entry:
Symmetrization (of tensors). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetrization_(of_tensors)&oldid=49463
This article was adapted from an original article by L.P. Kuptsov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Symmetrization_(of_tensors)&oldid=49463"