Difference between revisions of "Super-group"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48908 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''Lie super-group'' | ''Lie super-group'' | ||
| − | A group object in the category of super-manifolds (cf. [[Super-manifold|Super-manifold]]). A super-group | + | A group object in the category of super-manifolds (cf. [[Super-manifold|Super-manifold]]). A super-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911701.png" /> is defined by a functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911702.png" /> from the category of commutative superalgebras into the category of groups. Lie's theorems (cf. [[Lie theorem|Lie theorem]]) are transferred to super-groups, a fact that gives the correspondence between super-groups and finite-dimensional Lie superalgebras (cf. [[Superalgebra|Superalgebra]]). |
| − | is defined by a functor | ||
| − | from the category of commutative superalgebras into the category of groups. Lie's theorems (cf. [[Lie theorem|Lie theorem]]) are transferred to super-groups, a fact that gives the correspondence between super-groups and finite-dimensional Lie superalgebras (cf. [[Superalgebra|Superalgebra]]). | ||
===Examples.=== | ===Examples.=== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 1) The super-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911703.png" /> is defined by the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911704.png" /> into groups of even invertible matrices from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911705.png" /> (see [[Super-space|Super-space]]), i.e. of matrices in the form | |
| − | + | ||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911706.png" /></td> </tr></table> | ||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911707.png" /> are invertible matrices of orders <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911708.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s0911709.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117010.png" /> are matrices over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117011.png" />. A homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117012.png" /> is defined by the formula |
| − | are invertible matrices of orders | ||
| − | over | ||
| − | while | ||
| − | are matrices over | ||
| − | A homomorphism | ||
| − | is defined by the formula | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117013.png" /></td> </tr></table> | |
| − | |||
(the Berezinian); | (the Berezinian); | ||
| − | 2) | + | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117014.png" />; |
| − | 3) | + | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117016.png" />; they leave invariant an even, or odd, non-degenerate symmetric bilinear form. |
| − | and | ||
| − | they leave invariant an even, or odd, non-degenerate symmetric bilinear form. | ||
| − | To every super-group | + | To every super-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117017.png" /> and super-subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117018.png" /> of it there is related a super-manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117019.png" />, represented by a functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117020.png" />. This super-manifold is a homogeneous space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091170/s09117021.png" />. |
| − | and super-subgroup | ||
| − | of it there is related a super-manifold | ||
| − | represented by a functor | ||
| − | This super-manifold is a homogeneous space of | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Gauge fields and complex geometry" , Springer (1988) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.A. Berezin, "Introduction to superanalysis" , Reidel (1987) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.A. Leites (ed.) , ''Seminar on supermanifolds'' , Kluwer (1990)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Gauge fields and complex geometry" , Springer (1988) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.A. Berezin, "Introduction to superanalysis" , Reidel (1987) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.A. Leites (ed.) , ''Seminar on supermanifolds'' , Kluwer (1990)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
Lie super-group
A group object in the category of super-manifolds (cf. Super-manifold). A super-group  is defined by a functor
is defined by a functor  from the category of commutative superalgebras into the category of groups. Lie's theorems (cf. Lie theorem) are transferred to super-groups, a fact that gives the correspondence between super-groups and finite-dimensional Lie superalgebras (cf. Superalgebra).
from the category of commutative superalgebras into the category of groups. Lie's theorems (cf. Lie theorem) are transferred to super-groups, a fact that gives the correspondence between super-groups and finite-dimensional Lie superalgebras (cf. Superalgebra).
Examples.
1) The super-group 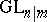 is defined by the functor
is defined by the functor  into groups of even invertible matrices from
into groups of even invertible matrices from  (see Super-space), i.e. of matrices in the form
(see Super-space), i.e. of matrices in the form
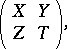 |
where  are invertible matrices of orders
are invertible matrices of orders  over
over  , while
, while 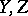 are matrices over
are matrices over  . A homomorphism
. A homomorphism 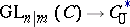 is defined by the formula
is defined by the formula
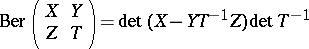 |
(the Berezinian);
2) 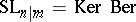 ;
;
3) 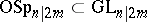 and
and 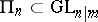 ; they leave invariant an even, or odd, non-degenerate symmetric bilinear form.
; they leave invariant an even, or odd, non-degenerate symmetric bilinear form.
To every super-group 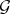 and super-subgroup
and super-subgroup 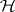 of it there is related a super-manifold
of it there is related a super-manifold 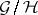 , represented by a functor
, represented by a functor 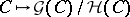 . This super-manifold is a homogeneous space of
. This super-manifold is a homogeneous space of 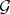 .
.
References
| [1] | Yu.I. Manin, "Gauge fields and complex geometry" , Springer (1988) (Translated from Russian) |
| [2] | F.A. Berezin, "Introduction to superanalysis" , Reidel (1987) (Translated from Russian) |
| [3] | D.A. Leites (ed.) , Seminar on supermanifolds , Kluwer (1990) |
Super-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Super-group&oldid=49457