Difference between revisions of "Stiefel manifold"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48838 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''(real)'' | ''(real)'' | ||
| − | The manifold | + | The manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877701.png" /> of orthonormal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877702.png" />-frames in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877703.png" />-dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877704.png" /> and a quaternion Stiefel manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877705.png" />. Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877706.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877707.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877708.png" />, respectively. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s0877709.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777011.png" /> are the spheres, the Stiefel manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777012.png" /> is the manifold of unit vectors tangent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777013.png" />, the Stiefel manifolds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777016.png" /> are identified with the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777018.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777019.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777020.png" /> — with the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777021.png" />. Sometimes non-compact Stiefel manifolds, consisting of all possible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777022.png" />-frames in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777024.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777025.png" />, are considered. |
| − | of orthonormal | ||
| − | frames in an | ||
| − | dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold | ||
| − | and a quaternion Stiefel manifold | ||
| − | Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups | ||
| − | |||
| − | and | ||
| − | respectively. In particular, | ||
| − | |||
| − | |||
| − | are the spheres, the Stiefel manifold | ||
| − | is the manifold of unit vectors tangent to | ||
| − | the Stiefel manifolds | ||
| − | |||
| − | |||
| − | are identified with the groups | ||
| − | |||
| − | |||
| − | and | ||
| − | with the group | ||
| − | Sometimes non-compact Stiefel manifolds, consisting of all possible | ||
| − | frames in | ||
| − | |||
| − | or | ||
| − | are considered. | ||
These manifolds were introduced by E. Stiefel [[#References|[1]]] in connection with systems of linearly independent vector fields on smooth manifolds. First started in [[#References|[1]]], studies on the topology of Stiefel manifolds led later to the complete calculation of their cohomology rings (see [[#References|[2]]], [[#References|[3]]]). In particular, | These manifolds were introduced by E. Stiefel [[#References|[1]]] in connection with systems of linearly independent vector fields on smooth manifolds. First started in [[#References|[1]]], studies on the topology of Stiefel manifolds led later to the complete calculation of their cohomology rings (see [[#References|[2]]], [[#References|[3]]]). In particular, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777026.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777027.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777028.png" /> is a commutative algebra with generators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777029.png" /> and relations | |
| − | is a commutative algebra with generators | ||
| − | and relations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777030.png" /></td> </tr></table> | |
| − | |||
| − | (everywhere above, | + | (everywhere above, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777031.png" /> denotes an element of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777032.png" />). Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777033.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777035.png" />, respectively. Moreover, |
| − | denotes an element of order | ||
| − | Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding | ||
| − | |||
| − | and | ||
| − | respectively. Moreover, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777036.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777037.png" /></td> </tr></table> | |
| − | |||
| − | |||
The computation of other homotopy groups of Stiefel manifolds is discussed in [[#References|[5]]]. | The computation of other homotopy groups of Stiefel manifolds is discussed in [[#References|[5]]]. | ||
| Line 75: | Line 23: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Stiefel, "Richtungsfelder und Fernparallelismus in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777038.png" />-dimensionalen Mannigfaltigkeiten" ''Comm. Math. Helv.'' , '''8''' : 4 (1935–1936) pp. 305–353</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, , ''Fibre spaces and their applications'' , Moscow (1958) pp. 163–246 (In Russian; translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom.'' (1971) pp. 71–122</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Stiefel, "Richtungsfelder und Fernparallelismus in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777038.png" />-dimensionalen Mannigfaltigkeiten" ''Comm. Math. Helv.'' , '''8''' : 4 (1935–1936) pp. 305–353</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, , ''Fibre spaces and their applications'' , Moscow (1958) pp. 163–246 (In Russian; translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom.'' (1971) pp. 71–122</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
For homotopy groups of Stiefel manifolds see also . | For homotopy groups of Stiefel manifolds see also . | ||
| − | Another (and better) frequently used notation for the Stiefel manifolds | + | Another (and better) frequently used notation for the Stiefel manifolds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777039.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777041.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777044.png" />, generalizing to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777045.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777046.png" /> is an appropriate vector space. |
| − | |||
| − | and | ||
| − | is | ||
| − | |||
| − | |||
| − | generalizing to | ||
| − | where | ||
| − | is an appropriate vector space. | ||
As homogeneous spaces these Stiefel manifolds are equal to, respectively, | As homogeneous spaces these Stiefel manifolds are equal to, respectively, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777047.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777048.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777049.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | The natural quotient mapping | + | The natural quotient mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777050.png" />, etc., assigns to an orthogonal, etc., matrix the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777051.png" />-frame consisting of its first <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777052.png" /> columns. |
| − | etc., assigns to an orthogonal, etc., matrix the | ||
| − | frame consisting of its first | ||
| − | columns. | ||
There are canonical mappings from the Stiefel manifolds to the Grassmann manifolds (cf. [[Grassmann manifold|Grassmann manifold]]): | There are canonical mappings from the Stiefel manifolds to the Grassmann manifolds (cf. [[Grassmann manifold|Grassmann manifold]]): | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777053.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | which assign to a | + | which assign to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777054.png" />-frame the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777055.png" />-dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces: |
| − | frame the | ||
| − | dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777056.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
etc. | etc. | ||
| − | Given an | + | Given an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777057.png" />-dimensional (real, complex, quaternionic) [[Vector bundle|vector bundle]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777058.png" /> over a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777059.png" />, the associated Stiefel bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777060.png" /> have the fibres <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777061.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777062.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777063.png" /> is the fibre of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777064.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777065.png" />. Similarly one has the Grassmann bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777066.png" />, whose fibre over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777067.png" /> is the Grassmann manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777068.png" />. |
| − | dimensional (real, complex, quaternionic) [[Vector bundle|vector bundle]] | ||
| − | over a space | ||
| − | the associated Stiefel bundles | ||
| − | have the fibres | ||
| − | over | ||
| − | where | ||
| − | is the fibre of | ||
| − | over | ||
| − | Similarly one has the Grassmann bundle | ||
| − | whose fibre over | ||
| − | is the Grassmann manifold | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989)</TD></TR><TR><TD valign="top">[a3a]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777069.png" />" ''Quarterly J. Math.'' , '''7''' (1956) pp. 249–268</TD></TR><TR><TD valign="top">[a3b]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777070.png" />" ''Quarterly J. Math.'' , '''9''' (1958) pp. 8–27</TD></TR><TR><TD valign="top">[a3c]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777071.png" />" ''Quarterly J. Math.'' , '''10''' (1959) pp. 17–37; 241–260</TD></TR><TR><TD valign="top">[a3d]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777072.png" />" ''Quarterly J. Math.'' , '''11''' (1960) pp. 1–16</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989)</TD></TR><TR><TD valign="top">[a3a]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777069.png" />" ''Quarterly J. Math.'' , '''7''' (1956) pp. 249–268</TD></TR><TR><TD valign="top">[a3b]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777070.png" />" ''Quarterly J. Math.'' , '''9''' (1958) pp. 8–27</TD></TR><TR><TD valign="top">[a3c]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777071.png" />" ''Quarterly J. Math.'' , '''10''' (1959) pp. 17–37; 241–260</TD></TR><TR><TD valign="top">[a3d]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777072.png" />" ''Quarterly J. Math.'' , '''11''' (1960) pp. 1–16</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
(real)
The manifold  of orthonormal
of orthonormal  -frames in an
-frames in an  -dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold
-dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold  and a quaternion Stiefel manifold
and a quaternion Stiefel manifold  . Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups
. Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups  ,
,  and
and  , respectively. In particular,
, respectively. In particular,  ,
,  ,
,  are the spheres, the Stiefel manifold
are the spheres, the Stiefel manifold  is the manifold of unit vectors tangent to
is the manifold of unit vectors tangent to  , the Stiefel manifolds
, the Stiefel manifolds  ,
,  ,
,  are identified with the groups
are identified with the groups  ,
,  ,
,  , and
, and  — with the group
— with the group 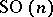 . Sometimes non-compact Stiefel manifolds, consisting of all possible
. Sometimes non-compact Stiefel manifolds, consisting of all possible  -frames in
-frames in  ,
, 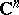 or
or  , are considered.
, are considered.
These manifolds were introduced by E. Stiefel [1] in connection with systems of linearly independent vector fields on smooth manifolds. First started in [1], studies on the topology of Stiefel manifolds led later to the complete calculation of their cohomology rings (see [2], [3]). In particular,
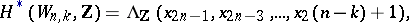 |
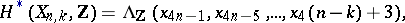 |
 is a commutative algebra with generators
is a commutative algebra with generators  and relations
and relations
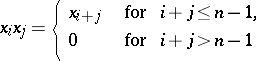 |
(everywhere above,  denotes an element of order
denotes an element of order  ). Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding
). Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding  ,
, 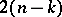 and
and  , respectively. Moreover,
, respectively. Moreover,
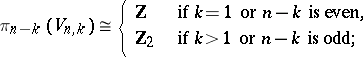 |
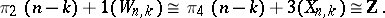 |
The computation of other homotopy groups of Stiefel manifolds is discussed in [5].
References
| [1] | E. Stiefel, "Richtungsfelder und Fernparallelismus in  -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 |
| [2] | A. Borel, , Fibre spaces and their applications , Moscow (1958) pp. 163–246 (In Russian; translated from French) |
| [3] | N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962) |
| [4] | V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian) |
| [5] | Itogi Nauk. Algebra. Topol. Geom. (1971) pp. 71–122 |
Comments
For homotopy groups of Stiefel manifolds see also .
Another (and better) frequently used notation for the Stiefel manifolds  ,
,  and
and 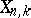 is
is  ,
,  ,
,  , generalizing to
, generalizing to 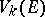 where
where  is an appropriate vector space.
is an appropriate vector space.
As homogeneous spaces these Stiefel manifolds are equal to, respectively,
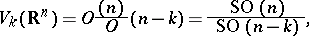 |
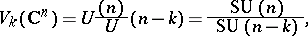 |
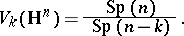 |
The natural quotient mapping  , etc., assigns to an orthogonal, etc., matrix the
, etc., assigns to an orthogonal, etc., matrix the  -frame consisting of its first
-frame consisting of its first  columns.
columns.
There are canonical mappings from the Stiefel manifolds to the Grassmann manifolds (cf. Grassmann manifold):
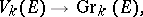 |
which assign to a 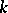 -frame the
-frame the 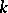 -dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces:
-dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces:
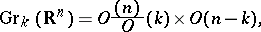 |
etc.
Given an  -dimensional (real, complex, quaternionic) vector bundle
-dimensional (real, complex, quaternionic) vector bundle 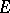 over a space
over a space  , the associated Stiefel bundles
, the associated Stiefel bundles  have the fibres
have the fibres 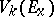 over
over  , where
, where  is the fibre of
is the fibre of 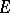 over
over  . Similarly one has the Grassmann bundle
. Similarly one has the Grassmann bundle  , whose fibre over
, whose fibre over 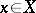 is the Grassmann manifold
is the Grassmann manifold 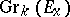 .
.
References
| [a1] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [a2] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
| [a3a] | G.F. Paechter, "The groups 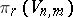 " Quarterly J. Math. , 7 (1956) pp. 249–268 " Quarterly J. Math. , 7 (1956) pp. 249–268 |
| [a3b] | G.F. Paechter, "The groups 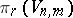 " Quarterly J. Math. , 9 (1958) pp. 8–27 " Quarterly J. Math. , 9 (1958) pp. 8–27 |
| [a3c] | G.F. Paechter, "The groups 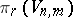 " Quarterly J. Math. , 10 (1959) pp. 17–37; 241–260 " Quarterly J. Math. , 10 (1959) pp. 17–37; 241–260 |
| [a3d] | G.F. Paechter, "The groups 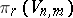 " Quarterly J. Math. , 11 (1960) pp. 1–16 " Quarterly J. Math. , 11 (1960) pp. 1–16 |
| [a4] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 |
| [a5] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) |
Stiefel manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stiefel_manifold&oldid=49446