Difference between revisions of "Statistical test"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48821 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A decision rule according to which a decision is taken in the problem of statistical hypotheses testing (cf. [[Statistical hypotheses, verification of|Statistical hypotheses, verification of]]) on the basis of results of observations. | A decision rule according to which a decision is taken in the problem of statistical hypotheses testing (cf. [[Statistical hypotheses, verification of|Statistical hypotheses, verification of]]) on the basis of results of observations. | ||
| − | Assume that the hypothesis | + | Assume that the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874801.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874802.png" /> has to be tested against the alternative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874803.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874804.png" /> by means of the realization <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874805.png" /> of a random vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874806.png" /> that takes values in a sample space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874807.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874808.png" />. Furthermore, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s0874809.png" /> be an arbitrary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748010.png" />-measurable function, mapping the sample space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748011.png" /> onto the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748012.png" />. In a case like this, the principle according to which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748013.png" /> is rejected with probability <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748014.png" />, while the alternative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748015.png" /> is rejected with probability <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748016.png" />, is called a statistical test for testing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748017.png" /> against <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748018.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748019.png" /> is the critical function of the test. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748021.png" />, is called the power function of the test. |
| − | |||
| − | has to be tested against the alternative | ||
| − | |||
| − | by means of the realization | ||
| − | of a random vector | ||
| − | that takes values in a sample space | ||
| − | |||
| − | Furthermore, let | ||
| − | be an arbitrary | ||
| − | measurable function, mapping the sample space | ||
| − | onto the interval | ||
| − | In a case like this, the principle according to which | ||
| − | is rejected with probability | ||
| − | while the alternative | ||
| − | is rejected with probability | ||
| − | is called a statistical test for testing | ||
| − | against | ||
| − | |||
| − | is the critical function of the test. The function | ||
| − | |||
| − | is called the power function of the test. | ||
| − | The use of a statistical test leads either to a correct decision being taken, or to one of the following two errors being made: rejection of | + | The use of a statistical test leads either to a correct decision being taken, or to one of the following two errors being made: rejection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748022.png" />, and thus acceptance of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748023.png" />, when in fact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748024.png" /> is correct (an error of the first kind), or acceptance of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748025.png" /> when in fact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748026.png" /> is correct (an error of the second kind). One of the basic problems in the classical theory of statistical hypotheses testing is the construction of a test that, given a definite upper bound <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748028.png" />, for the probability of an error of the first kind, would minimize the probability of an error of the second kind. The number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748029.png" /> is called the [[Significance level|significance level]] of the statistical test. |
| − | and thus acceptance of | ||
| − | when in fact | ||
| − | is correct (an error of the first kind), or acceptance of | ||
| − | when in fact | ||
| − | is correct (an error of the second kind). One of the basic problems in the classical theory of statistical hypotheses testing is the construction of a test that, given a definite upper bound | ||
| − | |||
| − | for the probability of an error of the first kind, would minimize the probability of an error of the second kind. The number | ||
| − | is called the [[Significance level|significance level]] of the statistical test. | ||
| − | In practice, the most important are non-randomized statistical tests, i.e. those with as critical function | + | In practice, the most important are non-randomized statistical tests, i.e. those with as critical function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748030.png" /> the indicator function of a certain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748031.png" />-measurable set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748032.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748033.png" />: |
| − | the indicator function of a certain | ||
| − | measurable set | ||
| − | in | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748034.png" /></td> </tr></table> | |
| − | |||
| − | Thus, a non-randomized statistical test rejects | + | Thus, a non-randomized statistical test rejects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748035.png" /> if the event <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748036.png" /> takes place; on the other hand, if the event <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748037.png" /> takes place, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748038.png" /> is accepted. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748039.png" /> is called the critical region of the statistical test. |
| − | if the event | ||
| − | takes place; on the other hand, if the event | ||
| − | takes place, then | ||
| − | is accepted. The set | ||
| − | is called the critical region of the statistical test. | ||
| − | As a rule, a non-randomized statistical test is based on a certain statistic | + | As a rule, a non-randomized statistical test is based on a certain statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748040.png" />, which is called the test statistic, and the critical region <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748041.png" /> of this same test is usually defined using relations of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748044.png" />. The constants <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748045.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748046.png" />, called the critical values of the test statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748047.png" />, are defined from the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748048.png" />; in these circumstances one speaks in the first two cases of one-sided statistical tests, and in the third case, of a two-sided statistical test. The structure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748049.png" /> reflects the particular nature of the competing hypotheses <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748050.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748051.png" />. In the case where the family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748052.png" /> possesses a sufficient statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748053.png" />, it is natural to look for the test statistic in the class of sufficient statistics, since |
| − | which is called the test statistic, and the critical region | ||
| − | of this same test is usually defined using relations of the form | ||
| − | |||
| − | |||
| − | The constants | ||
| − | |||
| − | called the critical values of the test statistic | ||
| − | are defined from the condition | ||
| − | in these circumstances one speaks in the first two cases of one-sided statistical tests, and in the third case, of a two-sided statistical test. The structure of | ||
| − | reflects the particular nature of the competing hypotheses | ||
| − | and | ||
| − | In the case where the family | ||
| − | possesses a sufficient statistic | ||
| − | it is natural to look for the test statistic in the class of sufficient statistics, since | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748054.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | for all | + | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748055.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087480/s08748056.png" />. |
| − | where | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.S. Nikulin, "A result of Bol'shev's from the theory of the statistical testing of hypotheses" ''J. Soviet Math.'' , '''44''' : 3 (1989) pp. 522–529 ''Zap. Nauchn. Sem. Mat. Inst. Steklov.'' , '''153''' (1986) pp. 129–137</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.S. Nikulin, "A result of Bol'shev's from the theory of the statistical testing of hypotheses" ''J. Soviet Math.'' , '''44''' : 3 (1989) pp. 522–529 ''Zap. Nauchn. Sem. Mat. Inst. Steklov.'' , '''153''' (1986) pp. 129–137</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
A decision rule according to which a decision is taken in the problem of statistical hypotheses testing (cf. Statistical hypotheses, verification of) on the basis of results of observations.
Assume that the hypothesis 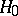 :
: 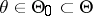 has to be tested against the alternative
has to be tested against the alternative 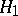 :
: 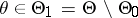 by means of the realization
by means of the realization 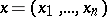 of a random vector
of a random vector 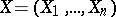 that takes values in a sample space
that takes values in a sample space 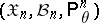 ,
, 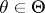 . Furthermore, let
. Furthermore, let 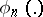 be an arbitrary
be an arbitrary 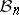 -measurable function, mapping the sample space
-measurable function, mapping the sample space 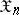 onto the interval
onto the interval 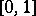 . In a case like this, the principle according to which
. In a case like this, the principle according to which 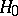 is rejected with probability
is rejected with probability 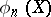 , while the alternative
, while the alternative 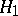 is rejected with probability
is rejected with probability 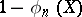 , is called a statistical test for testing
, is called a statistical test for testing 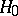 against
against 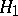 ;
; 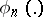 is the critical function of the test. The function
is the critical function of the test. The function 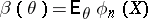 ,
, 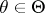 , is called the power function of the test.
, is called the power function of the test.
The use of a statistical test leads either to a correct decision being taken, or to one of the following two errors being made: rejection of 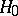 , and thus acceptance of
, and thus acceptance of 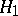 , when in fact
, when in fact 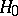 is correct (an error of the first kind), or acceptance of
is correct (an error of the first kind), or acceptance of 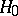 when in fact
when in fact 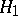 is correct (an error of the second kind). One of the basic problems in the classical theory of statistical hypotheses testing is the construction of a test that, given a definite upper bound
is correct (an error of the second kind). One of the basic problems in the classical theory of statistical hypotheses testing is the construction of a test that, given a definite upper bound  ,
, 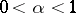 , for the probability of an error of the first kind, would minimize the probability of an error of the second kind. The number
, for the probability of an error of the first kind, would minimize the probability of an error of the second kind. The number 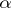 is called the significance level of the statistical test.
is called the significance level of the statistical test.
In practice, the most important are non-randomized statistical tests, i.e. those with as critical function 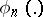 the indicator function of a certain
the indicator function of a certain 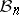 -measurable set
-measurable set 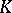 in
in 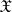 :
:
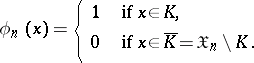 |
Thus, a non-randomized statistical test rejects 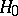 if the event
if the event 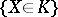 takes place; on the other hand, if the event
takes place; on the other hand, if the event 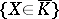 takes place, then
takes place, then 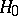 is accepted. The set
is accepted. The set 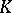 is called the critical region of the statistical test.
is called the critical region of the statistical test.
As a rule, a non-randomized statistical test is based on a certain statistic 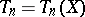 , which is called the test statistic, and the critical region
, which is called the test statistic, and the critical region 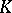 of this same test is usually defined using relations of the form
of this same test is usually defined using relations of the form 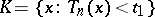 ,
, 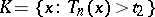 ,
, 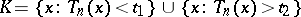 . The constants
. The constants 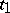 ,
, 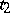 , called the critical values of the test statistic
, called the critical values of the test statistic 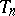 , are defined from the condition
, are defined from the condition 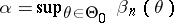 ; in these circumstances one speaks in the first two cases of one-sided statistical tests, and in the third case, of a two-sided statistical test. The structure of
; in these circumstances one speaks in the first two cases of one-sided statistical tests, and in the third case, of a two-sided statistical test. The structure of 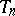 reflects the particular nature of the competing hypotheses
reflects the particular nature of the competing hypotheses  and
and 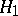 . In the case where the family
. In the case where the family 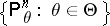 possesses a sufficient statistic
possesses a sufficient statistic 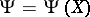 , it is natural to look for the test statistic in the class of sufficient statistics, since
, it is natural to look for the test statistic in the class of sufficient statistics, since
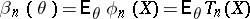 |
for all  , where
, where 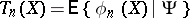 .
.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [2] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [3] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [4] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [5] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [6] | M.S. Nikulin, "A result of Bol'shev's from the theory of the statistical testing of hypotheses" J. Soviet Math. , 44 : 3 (1989) pp. 522–529 Zap. Nauchn. Sem. Mat. Inst. Steklov. , 153 (1986) pp. 129–137 |
Statistical test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_test&oldid=49445