Difference between revisions of "Simplicial object in a category"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48710 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853801.png" />'' |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A contravariant functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853802.png" /> (or, equivalently, a covariant functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853803.png" />) from the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853804.png" />, whose objects are ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853805.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853806.png" />, and whose morphisms are non-decreasing mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853807.png" />, into the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853808.png" />. A covariant functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s0853809.png" /> (or, equivalently, a contravariant functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538010.png" />) is called a co-simplicial object in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538011.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | A contravariant functor | ||
| − | or, equivalently, a covariant functor | ||
| − | from the category | ||
| − | whose objects are ordered sets | ||
| − | |||
| − | and whose morphisms are non-decreasing mappings | ||
| − | into the category | ||
| − | A covariant functor | ||
| − | or, equivalently, a contravariant functor | ||
| − | is called a co-simplicial object in | ||
The morphisms | The morphisms | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538012.png" /></td> </tr></table> | |
| − | |||
| − | 0 | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538013.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | of | + | of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538014.png" /> given by |
| − | given by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538015.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538016.png" /></td> </tr></table> | |
| − | |||
| − | generate all the morphisms of | + | generate all the morphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538017.png" />, so that a simplicial object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538018.png" /> is determined by the objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538020.png" /> (called the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538022.png" />-fibres or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538024.png" />-components of the simplicial object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538025.png" />), and the morphisms |
| − | so that a simplicial object | ||
| − | is determined by the objects | ||
| − | |||
| − | called the | ||
| − | fibres or | ||
| − | components of the simplicial object | ||
| − | and the morphisms | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538026.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | (called boundary operators and degeneracy operators, respectively). In case | + | (called boundary operators and degeneracy operators, respectively). In case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538027.png" /> is a category of structured sets, the elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538028.png" /> are usually called the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538030.png" />-dimensional simplices of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538031.png" />. The mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538033.png" /> satisfy the relations |
| − | is a category of structured sets, the elements of | ||
| − | are usually called the | ||
| − | dimensional simplices of | ||
| − | The mappings | ||
| − | and | ||
| − | satisfy the relations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538034.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | and any relation between these mappings is a consequence of the relations (*). This means that a simplicial object | + | and any relation between these mappings is a consequence of the relations (*). This means that a simplicial object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538035.png" /> can be identified with a system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538036.png" /> of objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538038.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538039.png" /> and morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538041.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538042.png" />, satisfying the relations |
| − | can be identified with a system | ||
| − | of objects | ||
| − | |||
| − | of | ||
| − | and morphisms | ||
| − | and | ||
| − | |||
| − | satisfying the relations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538043.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538044.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538045.png" /></td> </tr></table> | |
| − | |||
| − | Similarly, a co-simplicial object | + | Similarly, a co-simplicial object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538046.png" /> can be identified with a system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538047.png" /> of objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538048.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538049.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538051.png" />-co-fibres) and morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538053.png" /> (co-boundary operators), and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538055.png" /> (co-degeneracy operators), satisfying the relations (*) (with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538056.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538057.png" />). |
| − | can be identified with a system | ||
| − | of objects | ||
| − | |||
| − | |||
| − | co-fibres) and morphisms | ||
| − | |||
| − | co-boundary operators), and | ||
| − | |||
| − | co-degeneracy operators), satisfying the relations (*) (with | ||
| − | |||
| − | A simplicial mapping | + | A simplicial mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538058.png" /> between simplicial objects (in the same category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538059.png" />) is a transformation (morphism) of functors from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538060.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538061.png" />, that is, a family of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538062.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538063.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538064.png" /> such that |
| − | between simplicial objects (in the same category | ||
| − | is a transformation (morphism) of functors from | ||
| − | into | ||
| − | that is, a family of morphisms | ||
| − | |||
| − | of | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538065.png" /></td> </tr></table> | |
| − | |||
| − | 0 | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538066.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | The simplicial objects of | + | The simplicial objects of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538067.png" /> and their simplicial mappings form a category, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538068.png" />. |
| − | and their simplicial mappings form a category, denoted by | ||
| − | A simplicial homotopy | + | A simplicial homotopy <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538069.png" /> between two simplicial mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538070.png" /> between simplicial objects in a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538071.png" /> is a family of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538072.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538073.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538074.png" /> such that |
| − | between two simplicial mappings | ||
| − | between simplicial objects in a category | ||
| − | is a family of morphisms | ||
| − | |||
| − | of | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538075.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538076.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538077.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538078.png" /></td> </tr></table> | |
| − | s | ||
| − | On the basis of this definition one can reproduce in essence the whole of ordinary homotopy theory in the category | + | On the basis of this definition one can reproduce in essence the whole of ordinary homotopy theory in the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538079.png" />, for any category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538080.png" />. In the case of the category of sets or topological spaces, the geometric realization functor (see [[Simplicial set|Simplicial set]]) carries this "simplicial" theory into the usual one. |
| − | for any category | ||
| − | In the case of the category of sets or topological spaces, the geometric realization functor (see [[Simplicial set|Simplicial set]]) carries this "simplicial" theory into the usual one. | ||
Examples of simplicial objects are a simplicial set, a simplicial topological space, a simplicial algebraic variety, a simplicial group, a simplicial Abelian group, a simplicial Lie algebra, a simplicial smooth manifold, etc. | Examples of simplicial objects are a simplicial set, a simplicial topological space, a simplicial algebraic variety, a simplicial group, a simplicial Abelian group, a simplicial Lie algebra, a simplicial smooth manifold, etc. | ||
| − | Every simplicial Abelian group can be made into a chain complex with boundary operator | + | Every simplicial Abelian group can be made into a chain complex with boundary operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085380/s08538081.png" />. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.P. May, "Simplicial objects in algebraic topology" , v. Nostrand (1967)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> K. Lamotke, "Semisimpliziale algebraische Topologie" , Springer (1968)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.P. May, "Simplicial objects in algebraic topology" , v. Nostrand (1967)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> K. Lamotke, "Semisimpliziale algebraische Topologie" , Springer (1968)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
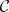
A contravariant functor 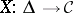 (or, equivalently, a covariant functor
(or, equivalently, a covariant functor 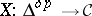 ) from the category
) from the category 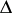 , whose objects are ordered sets
, whose objects are ordered sets 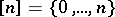 ,
, 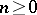 , and whose morphisms are non-decreasing mappings
, and whose morphisms are non-decreasing mappings 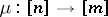 , into the category
, into the category 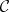 . A covariant functor
. A covariant functor 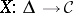 (or, equivalently, a contravariant functor
(or, equivalently, a contravariant functor  ) is called a co-simplicial object in
) is called a co-simplicial object in 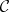 .
.
The morphisms
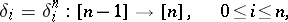 |
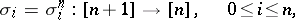 |
of  given by
given by
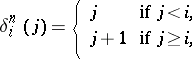 |
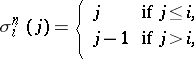 |
generate all the morphisms of 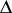 , so that a simplicial object
, so that a simplicial object 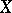 is determined by the objects
is determined by the objects 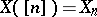 ,
, 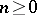 (called the
(called the  -fibres or
-fibres or  -components of the simplicial object
-components of the simplicial object 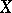 ), and the morphisms
), and the morphisms
 |
(called boundary operators and degeneracy operators, respectively). In case 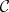 is a category of structured sets, the elements of
is a category of structured sets, the elements of 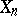 are usually called the
are usually called the  -dimensional simplices of
-dimensional simplices of 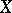 . The mappings
. The mappings 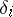 and
and 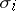 satisfy the relations
satisfy the relations
 | (*) |
and any relation between these mappings is a consequence of the relations (*). This means that a simplicial object 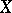 can be identified with a system
can be identified with a system 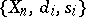 of objects
of objects 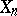 ,
, 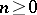 , of
, of 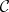 and morphisms
and morphisms 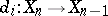 and
and 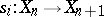 ,
, 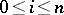 , satisfying the relations
, satisfying the relations
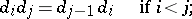 |
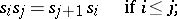 |
 |
Similarly, a co-simplicial object 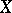 can be identified with a system
can be identified with a system 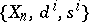 of objects
of objects 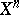 ,
, 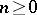 (
( -co-fibres) and morphisms
-co-fibres) and morphisms 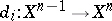 ,
, 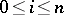 (co-boundary operators), and
(co-boundary operators), and 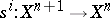 ,
, 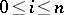 (co-degeneracy operators), satisfying the relations (*) (with
(co-degeneracy operators), satisfying the relations (*) (with 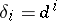 ,
, 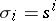 ).
).
A simplicial mapping  between simplicial objects (in the same category
between simplicial objects (in the same category 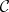 ) is a transformation (morphism) of functors from
) is a transformation (morphism) of functors from 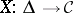 into
into 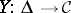 , that is, a family of morphisms
, that is, a family of morphisms 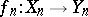 ,
, 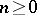 , of
, of  such that
such that
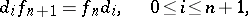 |
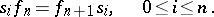 |
The simplicial objects of 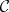 and their simplicial mappings form a category, denoted by
and their simplicial mappings form a category, denoted by 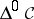 .
.
A simplicial homotopy 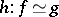 between two simplicial mappings
between two simplicial mappings 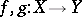 between simplicial objects in a category
between simplicial objects in a category 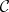 is a family of morphisms
is a family of morphisms 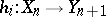 ,
, 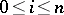 , of
, of 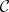 such that
such that
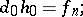 |
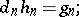 |
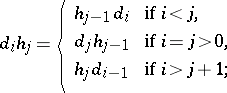 |
 |
On the basis of this definition one can reproduce in essence the whole of ordinary homotopy theory in the category 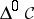 , for any category
, for any category 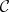 . In the case of the category of sets or topological spaces, the geometric realization functor (see Simplicial set) carries this "simplicial" theory into the usual one.
. In the case of the category of sets or topological spaces, the geometric realization functor (see Simplicial set) carries this "simplicial" theory into the usual one.
Examples of simplicial objects are a simplicial set, a simplicial topological space, a simplicial algebraic variety, a simplicial group, a simplicial Abelian group, a simplicial Lie algebra, a simplicial smooth manifold, etc.
Every simplicial Abelian group can be made into a chain complex with boundary operator 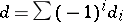 .
.
References
| [1] | P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967) |
| [2] | J.P. May, "Simplicial objects in algebraic topology" , v. Nostrand (1967) |
| [3] | K. Lamotke, "Semisimpliziale algebraische Topologie" , Springer (1968) |
Simplicial object in a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simplicial_object_in_a_category&oldid=49427