Difference between revisions of "Riemannian connection"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48557 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | An [[Affine connection|affine connection]] on a [[Riemannian space|Riemannian space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821101.png" /> with respect to which the [[Metric tensor|metric tensor]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821102.png" /> of the space is covariantly constant. If the affine connection on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821103.png" /> is given by a matrix of local connection forms |
| − | r0821101.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821104.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | + | and the metric form on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821105.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821106.png" />, then the latter condition is expressed as | |
| − | |||
| − | |||
| − | is | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821107.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | + | It can be also expressed as follows: Under [[Parallel displacement(2)|parallel displacement]] along any curve in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821108.png" />, the scalar product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r0821109.png" /> of two arbitrary vectors preserves its value, i.e. for vector fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211010.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211011.png" /> the following equality holds: | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211012.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211013.png" /> is the vector field, called the [[Covariant derivative|covariant derivative]] of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211014.png" /> relative to the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211015.png" />, defined by the formula | |
| − | the | ||
| − | |||
| − | |||
| − | the | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211016.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | If in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211017.png" /> one goes over to a local field of orthonormal frames, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211018.png" /> (if one restricts to the case of a positive-definite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211019.png" />) and condition (2) takes the form | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211020.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | i.e. the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211021.png" /> of forms (1) takes values in the Lie algebra of the group of motions of the Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211022.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211023.png" />. Thus, a Riemannian connection can be interpreted as a connection in the fibre space of orthonormal frames in the Euclidean spaces tangent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211024.png" />. The [[Holonomy group|holonomy group]] of a Riemannian connection is a subgroup of the group of motions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211025.png" />; a Riemannian connection for some Riemannian metric on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211026.png" /> is any affine connection whose holonomy group is the group of motions or some subgroup of it. | |
| − | |||
| − | |||
| − | |||
| − | + | If in (1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211027.png" /> (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211028.png" /> is considered with respect to the field of natural frames of a local coordinate system), then | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211029.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
and | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211030.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211031.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | is the so-called [[Christoffel symbol|Christoffel symbol]] and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211032.png" /> is the [[Torsion tensor|torsion tensor]] of the Riemannian connection. There exists one and only one Riemannian connection without torsion (i.e. such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211033.png" />); it is determined by the forms | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082110/r08211034.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
and it is called the [[Levi-Civita connection|Levi-Civita connection]]. | and it is called the [[Levi-Civita connection|Levi-Civita connection]]. | ||
| Line 124: | Line 41: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
Revision as of 14:53, 7 June 2020
An affine connection on a Riemannian space 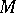 with respect to which the metric tensor
with respect to which the metric tensor  of the space is covariantly constant. If the affine connection on
of the space is covariantly constant. If the affine connection on  is given by a matrix of local connection forms
is given by a matrix of local connection forms
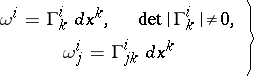 | (1) |
and the metric form on  is
is  , then the latter condition is expressed as
, then the latter condition is expressed as
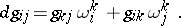 | (2) |
It can be also expressed as follows: Under parallel displacement along any curve in  , the scalar product
, the scalar product  of two arbitrary vectors preserves its value, i.e. for vector fields
of two arbitrary vectors preserves its value, i.e. for vector fields  on
on 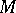 the following equality holds:
the following equality holds:
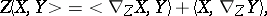 |
where 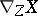 is the vector field, called the covariant derivative of the field
is the vector field, called the covariant derivative of the field  relative to the field
relative to the field 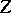 , defined by the formula
, defined by the formula
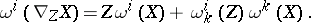 |
If in 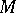 one goes over to a local field of orthonormal frames, then
one goes over to a local field of orthonormal frames, then  (if one restricts to the case of a positive-definite
(if one restricts to the case of a positive-definite 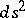 ) and condition (2) takes the form
) and condition (2) takes the form
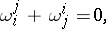 |
i.e. the matrix 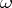 of forms (1) takes values in the Lie algebra of the group of motions of the Euclidean space
of forms (1) takes values in the Lie algebra of the group of motions of the Euclidean space 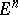 of dimension
of dimension  . Thus, a Riemannian connection can be interpreted as a connection in the fibre space of orthonormal frames in the Euclidean spaces tangent to
. Thus, a Riemannian connection can be interpreted as a connection in the fibre space of orthonormal frames in the Euclidean spaces tangent to  . The holonomy group of a Riemannian connection is a subgroup of the group of motions of
. The holonomy group of a Riemannian connection is a subgroup of the group of motions of 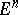 ; a Riemannian connection for some Riemannian metric on
; a Riemannian connection for some Riemannian metric on 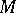 is any affine connection whose holonomy group is the group of motions or some subgroup of it.
is any affine connection whose holonomy group is the group of motions or some subgroup of it.
If in (1) 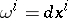 (i.e.
(i.e. 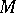 is considered with respect to the field of natural frames of a local coordinate system), then
is considered with respect to the field of natural frames of a local coordinate system), then
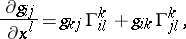 |
and
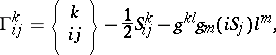 |
where
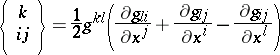 |
is the so-called Christoffel symbol and  is the torsion tensor of the Riemannian connection. There exists one and only one Riemannian connection without torsion (i.e. such that
is the torsion tensor of the Riemannian connection. There exists one and only one Riemannian connection without torsion (i.e. such that 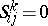 ); it is determined by the forms
); it is determined by the forms
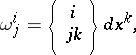 |
and it is called the Levi-Civita connection.
References
| [1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [2] | A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French) |
Comments
Instead of "Riemannian connection" one also uses metric connection.
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
Riemannian connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemannian_connection&oldid=49405