Difference between revisions of "Riemann hypothesis, generalized"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48548 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A statement about the non-trivial zeros of Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819401.png" />-functions (cf. [[Dirichlet L-function|Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819402.png" />-function]]), Dedekind zeta-functions (cf. [[Zeta-function|Zeta-function]]) and several other similar functions, similar to the Riemann hypothesis (cf. [[Riemann hypotheses|Riemann hypotheses]]) on the non-trivial zeros of the Riemann zeta-function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819403.png" />. In the case of Dirichlet zeta-functions the generalized Riemann hypothesis is called the extended Riemann hypothesis. |
| − | r0819401.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | --> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | For Dirichlet | + | For Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819404.png" />-functions it is not even known whether there exist real zeros in the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819405.png" /> (Siegel zeros). This is important in connection with the class number of quadratic fields (see also [[Quadratic field|Quadratic field]]; [[Siegel theorem|Siegel theorem]]). |
| − | functions it is not even known whether there exist real zeros in the interval | ||
| − | Siegel zeros). This is important in connection with the class number of quadratic fields (see also [[Quadratic field|Quadratic field]]; [[Siegel theorem|Siegel theorem]]). | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819407.png" /> be an algebraic number field, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819408.png" /> the group of fractional ideals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r0819409.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194010.png" /> its idèle class group (cf. [[Idèle|Idèle]]; [[Fractional ideal|Fractional ideal]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194011.png" /> be a quasi-character on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194012.png" />, i.e. a continuous homomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194013.png" /> into the group of non-zero complex numbers. Then for an idèle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194014.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194015.png" />, where for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194017.png" /> is a quasi-character of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194018.png" /> which is equal to unity on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194019.png" />, the units of the local completion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194020.png" />, for almost-all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194021.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194022.png" /> be a finite subset of the valuations on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194023.png" /> including the Archimedian ones, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194024.png" />. A function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194025.png" /> can now be defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194026.png" /> by setting for all prime ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194027.png" />, |
| − | be an algebraic number field, | ||
| − | the group of fractional ideals of | ||
| − | and | ||
| − | its idèle class group (cf. [[Idèle|Idèle]]; [[Fractional ideal|Fractional ideal]]). Let | ||
| − | be a quasi-character on | ||
| − | i.e. a continuous homomorphism of | ||
| − | into the group of non-zero complex numbers. Then for an idèle | ||
| − | one has | ||
| − | where for each | ||
| − | |||
| − | is a quasi-character of | ||
| − | which is equal to unity on | ||
| − | the units of the local completion | ||
| − | for almost-all | ||
| − | Let | ||
| − | be a finite subset of the valuations on | ||
| − | including the Archimedian ones, | ||
| − | A function | ||
| − | can now be defined on | ||
| − | by setting for all prime ideals | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194028.png" /></td> </tr></table> | |
| − | |||
| − | and extending | + | and extending <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194029.png" /> multiplicatively. These functions are called Hecke characters or Grössencharakters. Given such a character, the Hecke zeta-function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194030.png" /> is defined by |
| − | multiplicatively. These functions are called Hecke characters or Grössencharakters. Given such a character, the Hecke zeta-function of | ||
| − | is defined by | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194031.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194032.png" /> is the absolute norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194033.png" />. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194034.png" /> is also called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194036.png" />-series, Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194038.png" />-series (when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194039.png" /> is a Dirichlet character) or Hecke <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194041.png" />-function with Grössencharakter; it is also denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194042.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194043.png" /> one obtains the Dedekind <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194045.png" />-function. For Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194046.png" />-series the generalized Riemann hypothesis states that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194047.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194048.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | is the absolute norm | ||
| − | The function | ||
| − | is also called | ||
| − | series, Dirichlet | ||
| − | series (when | ||
| − | is a Dirichlet character) or Hecke | ||
| − | function with Grössencharakter; it is also denoted by | ||
| − | If | ||
| − | one obtains the Dedekind | ||
| − | function. For Dirichlet | ||
| − | series the generalized Riemann hypothesis states that | ||
| − | if | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Heilbronn, "Zeta-functions and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194049.png" />-functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1967) pp. 204–230</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. Chapt. 7, §1</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Heilbronn, "Zeta-functions and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081940/r08194049.png" />-functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , ''Algebraic number theory'' , Acad. Press (1967) pp. 204–230</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. Chapt. 7, §1</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
A statement about the non-trivial zeros of Dirichlet  -functions (cf. Dirichlet
-functions (cf. Dirichlet  -function), Dedekind zeta-functions (cf. Zeta-function) and several other similar functions, similar to the Riemann hypothesis (cf. Riemann hypotheses) on the non-trivial zeros of the Riemann zeta-function
-function), Dedekind zeta-functions (cf. Zeta-function) and several other similar functions, similar to the Riemann hypothesis (cf. Riemann hypotheses) on the non-trivial zeros of the Riemann zeta-function  . In the case of Dirichlet zeta-functions the generalized Riemann hypothesis is called the extended Riemann hypothesis.
. In the case of Dirichlet zeta-functions the generalized Riemann hypothesis is called the extended Riemann hypothesis.
Comments
For Dirichlet  -functions it is not even known whether there exist real zeros in the interval
-functions it is not even known whether there exist real zeros in the interval  (Siegel zeros). This is important in connection with the class number of quadratic fields (see also Quadratic field; Siegel theorem).
(Siegel zeros). This is important in connection with the class number of quadratic fields (see also Quadratic field; Siegel theorem).
Let  be an algebraic number field,
be an algebraic number field,  the group of fractional ideals of
the group of fractional ideals of  and
and  its idèle class group (cf. Idèle; Fractional ideal). Let
its idèle class group (cf. Idèle; Fractional ideal). Let  be a quasi-character on
be a quasi-character on 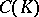 , i.e. a continuous homomorphism of
, i.e. a continuous homomorphism of  into the group of non-zero complex numbers. Then for an idèle
into the group of non-zero complex numbers. Then for an idèle  one has
one has  , where for each
, where for each  ,
, 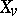 is a quasi-character of
is a quasi-character of  which is equal to unity on
which is equal to unity on  , the units of the local completion
, the units of the local completion 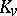 , for almost-all
, for almost-all  . Let
. Let  be a finite subset of the valuations on
be a finite subset of the valuations on  including the Archimedian ones,
including the Archimedian ones,  . A function
. A function 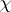 can now be defined on
can now be defined on 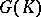 by setting for all prime ideals
by setting for all prime ideals 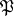 ,
,
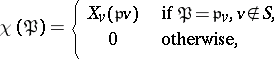 |
and extending  multiplicatively. These functions are called Hecke characters or Grössencharakters. Given such a character, the Hecke zeta-function of
multiplicatively. These functions are called Hecke characters or Grössencharakters. Given such a character, the Hecke zeta-function of  is defined by
is defined by
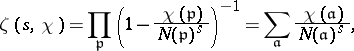 |
where  is the absolute norm
is the absolute norm  . The function
. The function  is also called
is also called  -series, Dirichlet
-series, Dirichlet 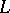 -series (when
-series (when  is a Dirichlet character) or Hecke
is a Dirichlet character) or Hecke 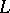 -function with Grössencharakter; it is also denoted by
-function with Grössencharakter; it is also denoted by  . If
. If 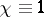 one obtains the Dedekind
one obtains the Dedekind  -function. For Dirichlet
-function. For Dirichlet  -series the generalized Riemann hypothesis states that
-series the generalized Riemann hypothesis states that  if
if  .
.
References
| [a1] | H. Heilbronn, "Zeta-functions and 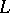 -functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) pp. 204–230 -functions" J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967) pp. 204–230 |
| [a2] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. Chapt. 7, §1 |
Riemann hypothesis, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_hypothesis,_generalized&oldid=49403