Difference between revisions of "Reflection"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48468 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805101.png" /> of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805102.png" />-dimensional simply-connected space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805103.png" /> of constant curvature (i.e. of a Euclidean or affine space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805104.png" />, a sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805105.png" /> or a hyperbolic (Lobachevskii) space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805106.png" />) the set of fixed points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805107.png" /> of which is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805108.png" />-dimensional hyperplane. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r0805109.png" /> is called the mirror of the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051010.png" />; in other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051011.png" /> is a reflection in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051012.png" />. Every reflection is uniquely defined by its mirror. The order (period) of a reflection in the group of all motions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051013.png" /> is equal to 2, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051014.png" />. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The Euclidean or affine space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051015.png" /> can be identified with the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051016.png" /> of its parallel translations. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051017.png" /> is then a linear orthogonal transformation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051018.png" /> with matrix | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051019.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | in a certain orthonormal basis, and conversely, every orthogonal transformation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051020.png" /> with this matrix in a certain orthonormal basis is a reflection in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051021.png" />. More generally, a linear transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051022.png" /> of an arbitrary vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051023.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051024.png" />, of characteristic other than 2, is called a linear reflection if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051025.png" /> and if the rank of the transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051026.png" /> is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051027.png" />. In this case, the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051028.png" /> of fixed vectors relative to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051029.png" /> has codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051030.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051031.png" />, the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051032.png" /> of eigenvectors with eigenvalue <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051033.png" /> has dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051035.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051036.png" /> is a linear form on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051037.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051038.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051039.png" />, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051040.png" /> is an element such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051041.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051042.png" /> is defined by the formula | |
| − | |||
| − | of | ||
| − | is | ||
| − | with | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051043.png" /></td> </tr></table> | |
| − | |||
| − | + | The description of a reflection in an arbitrary simply-connected space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051044.png" /> of constant curvature can be reduced to the description of linear reflections in the following way. Every such space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051045.png" /> can be imbedded as a hypersurface in a real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051046.png" />-dimensional vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051047.png" /> in such a way that the motions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051048.png" /> can be extended to linear transformations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051049.png" />. Moreover, in a suitable coordinate system in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051050.png" /> the equations of the hypersurface can be written in the following way: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | in | ||
| − | the | ||
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051051.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051052.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051053.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | Every hypersurface in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051054.png" />, given this imbedding, is the intersection with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051055.png" /> of a certain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051056.png" />-dimensional subspace in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051057.png" />, and every reflection in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051058.png" /> is induced by a linear reflection in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051059.png" />. | |
| − | |||
| − | |||
| − | + | If, in the definition of a linear reflection, the requirement that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051060.png" /> is dropped, then the more general concept of a pseudo-reflection is obtained. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051061.png" /> is the field of complex numbers and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051062.png" /> is a pseudo-reflection of finite order (not necessarily equal to 2), then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080510/r08051063.png" /> is called a unitary reflection. Every biholomorphic automorphism of finite order of a bounded symmetric domain in a complex space the set of fixed points of which has a complex codimension 1 is also called a unitary reflection. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | If, in the definition of a linear reflection, the requirement that | ||
| − | is dropped, then the more general concept of a pseudo-reflection is obtained. If | ||
| − | is the field of complex numbers and | ||
| − | is a pseudo-reflection of finite order (not necessarily equal to 2), then | ||
| − | is called a unitary reflection. Every biholomorphic automorphism of finite order of a bounded symmetric domain in a complex space the set of fixed points of which has a complex codimension 1 is also called a unitary reflection. | ||
See also [[Reflection group|Reflection group]]. | See also [[Reflection group|Reflection group]]. | ||
| Line 104: | Line 25: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Groupes et algèbres de Lie" , ''Eléments de mathématiques'' , Hermann (1968) pp. Chapts. 4–6</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.B. Vinberg, "Discrete linear groups generated by reflections" ''Math. USSR Izv.'' , '''35''' : 5 (1971) pp. 1083–1119 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''35''' : 5 (1971) pp. 1072–1112</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E. Gottschling, "Reflections in bounded symmetric domains" ''Comm. Pure Appl. Math.'' , '''22''' (1969) pp. 693–714</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Groupes et algèbres de Lie" , ''Eléments de mathématiques'' , Hermann (1968) pp. Chapts. 4–6</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.B. Vinberg, "Discrete linear groups generated by reflections" ''Math. USSR Izv.'' , '''35''' : 5 (1971) pp. 1083–1119 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''35''' : 5 (1971) pp. 1072–1112</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E. Gottschling, "Reflections in bounded symmetric domains" ''Comm. Pure Appl. Math.'' , '''22''' (1969) pp. 693–714</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
Revision as of 14:53, 7 June 2020
A mapping  of an
of an  -dimensional simply-connected space
-dimensional simply-connected space  of constant curvature (i.e. of a Euclidean or affine space
of constant curvature (i.e. of a Euclidean or affine space  , a sphere
, a sphere  or a hyperbolic (Lobachevskii) space
or a hyperbolic (Lobachevskii) space  ) the set of fixed points
) the set of fixed points  of which is an
of which is an  -dimensional hyperplane. The set
-dimensional hyperplane. The set  is called the mirror of the mapping
is called the mirror of the mapping  ; in other words,
; in other words,  is a reflection in
is a reflection in 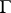 . Every reflection is uniquely defined by its mirror. The order (period) of a reflection in the group of all motions of
. Every reflection is uniquely defined by its mirror. The order (period) of a reflection in the group of all motions of 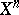 is equal to 2, i.e.
is equal to 2, i.e.  .
.
The Euclidean or affine space 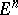 can be identified with the vector space
can be identified with the vector space 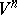 of its parallel translations. The mapping
of its parallel translations. The mapping 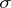 is then a linear orthogonal transformation of
is then a linear orthogonal transformation of 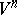 with matrix
with matrix
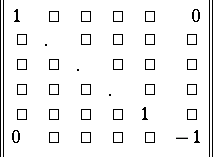 |
in a certain orthonormal basis, and conversely, every orthogonal transformation of  with this matrix in a certain orthonormal basis is a reflection in
with this matrix in a certain orthonormal basis is a reflection in 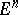 . More generally, a linear transformation
. More generally, a linear transformation 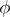 of an arbitrary vector space
of an arbitrary vector space 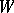 over a field
over a field 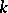 , of characteristic other than 2, is called a linear reflection if
, of characteristic other than 2, is called a linear reflection if 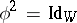 and if the rank of the transformation
and if the rank of the transformation 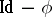 is equal to
is equal to 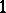 . In this case, the subspace
. In this case, the subspace  of fixed vectors relative to
of fixed vectors relative to  has codimension
has codimension  in
in  , the subspace
, the subspace 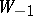 of eigenvectors with eigenvalue
of eigenvectors with eigenvalue 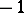 has dimension
has dimension 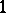 and
and 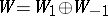 . If
. If 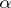 is a linear form on
is a linear form on  such that
such that 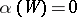 when
when 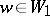 , and if
, and if 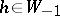 is an element such that
is an element such that 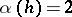 , then
, then  is defined by the formula
is defined by the formula
 |
The description of a reflection in an arbitrary simply-connected space 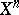 of constant curvature can be reduced to the description of linear reflections in the following way. Every such space
of constant curvature can be reduced to the description of linear reflections in the following way. Every such space  can be imbedded as a hypersurface in a real
can be imbedded as a hypersurface in a real 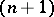 -dimensional vector space
-dimensional vector space  in such a way that the motions of
in such a way that the motions of 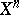 can be extended to linear transformations of
can be extended to linear transformations of 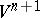 . Moreover, in a suitable coordinate system in
. Moreover, in a suitable coordinate system in 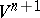 the equations of the hypersurface can be written in the following way:
the equations of the hypersurface can be written in the following way:
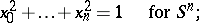 |
 |
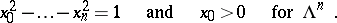 |
Every hypersurface in 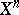 , given this imbedding, is the intersection with
, given this imbedding, is the intersection with 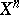 of a certain
of a certain  -dimensional subspace in
-dimensional subspace in 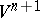 , and every reflection in
, and every reflection in 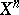 is induced by a linear reflection in
is induced by a linear reflection in 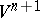 .
.
If, in the definition of a linear reflection, the requirement that  is dropped, then the more general concept of a pseudo-reflection is obtained. If
is dropped, then the more general concept of a pseudo-reflection is obtained. If 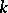 is the field of complex numbers and
is the field of complex numbers and 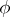 is a pseudo-reflection of finite order (not necessarily equal to 2), then
is a pseudo-reflection of finite order (not necessarily equal to 2), then 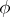 is called a unitary reflection. Every biholomorphic automorphism of finite order of a bounded symmetric domain in a complex space the set of fixed points of which has a complex codimension 1 is also called a unitary reflection.
is called a unitary reflection. Every biholomorphic automorphism of finite order of a bounded symmetric domain in a complex space the set of fixed points of which has a complex codimension 1 is also called a unitary reflection.
See also Reflection group.
References
| [1] | N. Bourbaki, "Groupes et algèbres de Lie" , Eléments de mathématiques , Hermann (1968) pp. Chapts. 4–6 |
| [2] | E.B. Vinberg, "Discrete linear groups generated by reflections" Math. USSR Izv. , 35 : 5 (1971) pp. 1083–1119 Izv. Akad. Nauk SSSR Ser. Mat. , 35 : 5 (1971) pp. 1072–1112 |
| [3] | E. Gottschling, "Reflections in bounded symmetric domains" Comm. Pure Appl. Math. , 22 (1969) pp. 693–714 |
| [4] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
The spelling reflexion also occurs in the literature.
A basic fact is that the reflections generate the orthogonal group; see [a2], Sects. 8.12.12, 13.7.12.
References
| [a1] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
| [a2] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a3] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a4] | M. Greenberg, "Euclidean and non-euclidean geometry" , Freeman (1980) |
| [a5] | B. Artmann, "Lineare Algebra" , Birkhäuser (1986) |
| [a6] | P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958) |
Reflection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reflection&oldid=49397