Difference between revisions of "Recursive relation"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48461 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A [[Relation|relation]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803201.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803202.png" /> is the set of natural numbers, such that the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803203.png" /> defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803204.png" /> by the condition |
| − | r0803201.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803205.png" /></td> </tr></table> | |
| − | |||
| − | + | is a [[Recursive function|recursive function]]. In particular, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803206.png" />, the universal relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803207.png" /> and the zero relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803208.png" /> are recursive relations. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r0803209.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032010.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032011.png" />-place recursive relations, then the relations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032015.png" /> will also be recursive relations. With regard to the operations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032018.png" />, the system of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080320/r08032019.png" />-place recursive relations thus forms a [[Boolean algebra|Boolean algebra]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | is a [[Recursive function|recursive function]]. In particular, for any | ||
| − | the universal relation | ||
| − | and the zero relation | ||
| − | are recursive relations. If | ||
| − | and | ||
| − | are | ||
| − | place recursive relations, then the relations | ||
| − | |||
| − | |||
| − | |||
| − | will also be recursive relations. With regard to the operations | ||
| − | |||
| − | |||
| − | the system of all | ||
| − | place recursive relations thus forms a [[Boolean algebra|Boolean algebra]]. | ||
Revision as of 14:53, 7 June 2020
A relation 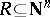 , where
, where 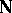 is the set of natural numbers, such that the function
is the set of natural numbers, such that the function 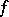 defined on
defined on 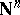 by the condition
by the condition
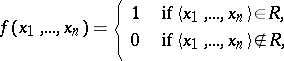 |
is a recursive function. In particular, for any  , the universal relation
, the universal relation 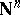 and the zero relation
and the zero relation 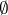 are recursive relations. If
are recursive relations. If 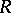 and
and 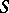 are
are  -place recursive relations, then the relations
-place recursive relations, then the relations 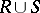 ,
, 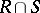 ,
, 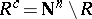 ,
, 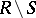 will also be recursive relations. With regard to the operations
will also be recursive relations. With regard to the operations  ,
, 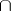 ,
,  , the system of all
, the system of all  -place recursive relations thus forms a Boolean algebra.
-place recursive relations thus forms a Boolean algebra.
How to Cite This Entry:
Recursive relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursive_relation&oldid=49396
Recursive relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursive_relation&oldid=49396
This article was adapted from an original article by V.E. Plisko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article