Difference between revisions of "Projective representation"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48325 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | ''of a group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753201.png" />'' |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A homomorphism of this group into the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753202.png" /> of projective transformations of the projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753203.png" /> associated to a vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753204.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753205.png" />. | |
| − | |||
| − | + | With each projective representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753206.png" /> of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753207.png" /> there is associated a central extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753208.png" />: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p0753209.png" /> be the [[General linear group|general linear group]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532010.png" />. Then one has a natural [[Exact sequence|exact sequence]] | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532011.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532012.png" /> is the natural projection of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532013.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532015.png" /> is the imbedding of the multiplicative group of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532016.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532017.png" /> by scalar matrices. The pullback along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532018.png" /> gives rise to the following commutative diagram with exact rows: | |
| − | of the group | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532019.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | which is the associated central extension. Every section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532020.png" />, i.e. homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532021.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532022.png" />, has the property | |
| − | is the | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532023.png" /></td> </tr></table> | |
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532024.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532025.png" />-cocycle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532026.png" />. The cohomology class of this cocycle is independent of the choice of the section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532027.png" />. It is determined by the projective representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532028.png" /> and determines the equivalence class of the extension (*). The condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532029.png" /> is necessary and sufficient for the projective representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532030.png" /> to be the composition of a linear representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532031.png" /> with the projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532032.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | cocycle of | ||
| − | The cohomology class of this cocycle is independent of the choice of the section | ||
| − | It is determined by the projective representation | ||
| − | and determines the equivalence class of the extension (*). The condition | ||
| − | is necessary and sufficient for the projective representation | ||
| − | to be the composition of a linear representation of | ||
| − | with the projection | ||
Projective representations arise naturally in studying linear representations of group extensions. The most important examples of projective representations are: the spinor representation of an orthogonal group and the Weyl representation of a symplectic group. The definitions of equivalence and irreducibility of representations carry over directly to projective representations. The classification of the irreducible projective representations of finite groups was obtained by I. Schur (1904). | Projective representations arise naturally in studying linear representations of group extensions. The most important examples of projective representations are: the spinor representation of an orthogonal group and the Weyl representation of a symplectic group. The definitions of equivalence and irreducibility of representations carry over directly to projective representations. The classification of the irreducible projective representations of finite groups was obtained by I. Schur (1904). | ||
| − | A projective representation is said to be unitary if | + | A projective representation is said to be unitary if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532033.png" /> is a Hilbert space and if the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532034.png" /> can be chosen so that it takes values in the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532035.png" /> of unitary operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532036.png" />. Irreducible unitary projective representations of topological groups have been studied [[#References|[4]]]; for a connected Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532037.png" /> this study reduces to a study of the irreducible unitary representations of a simply-connected Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532038.png" />, the Lie algebra of which is the central extension of the Lie algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532039.png" /> of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532040.png" /> by a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532041.png" />-dimensional commutative Lie algebra, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075320/p07532042.png" />. |
| − | is a Hilbert space and if the mapping | ||
| − | can be chosen so that it takes values in the group | ||
| − | of unitary operators on | ||
| − | Irreducible unitary projective representations of topological groups have been studied [[#References|[4]]]; for a connected Lie group | ||
| − | this study reduces to a study of the irreducible unitary representations of a simply-connected Lie group | ||
| − | the Lie algebra of which is the central extension of the Lie algebra | ||
| − | of the group | ||
| − | by a | ||
| − | dimensional commutative Lie algebra, where | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.W. Mackey, "Unitary representations of group extensions, I" ''Acta Math.'' , '''99''' (1958) pp. 265–311</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V. Bargmann, "Irreducible unitary representations of the Lorentz group" ''Ann. of Math.'' , '''48''' (1947) pp. 568–640</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.W. Mackey, "Unitary representations of group extensions, I" ''Acta Math.'' , '''99''' (1958) pp. 265–311</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V. Bargmann, "Irreducible unitary representations of the Lorentz group" ''Ann. of Math.'' , '''48''' (1947) pp. 568–640</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| + | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Methods of representation theory" , '''1–2''' , Wiley (Interscience) (1981–1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.M. Isaacs, "Character theory of finite groups" , Acad. Press (1976)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Methods of representation theory" , '''1–2''' , Wiley (Interscience) (1981–1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.M. Isaacs, "Character theory of finite groups" , Acad. Press (1976)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
of a group 
A homomorphism of this group into the group  of projective transformations of the projective space
of projective transformations of the projective space  associated to a vector space
associated to a vector space  over a field
over a field  .
.
With each projective representation  of the group
of the group 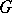 there is associated a central extension of
there is associated a central extension of  : Let
: Let  be the general linear group of
be the general linear group of 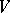 . Then one has a natural exact sequence
. Then one has a natural exact sequence
 |
where 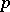 is the natural projection of the group
is the natural projection of the group 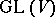 onto
onto 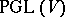 and
and 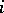 is the imbedding of the multiplicative group of the field
is the imbedding of the multiplicative group of the field 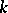 into
into 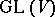 by scalar matrices. The pullback along
by scalar matrices. The pullback along 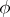 gives rise to the following commutative diagram with exact rows:
gives rise to the following commutative diagram with exact rows:
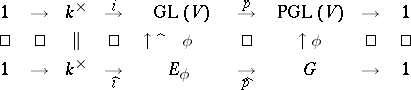 | (*) |
which is the associated central extension. Every section 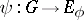 , i.e. homomorphism
, i.e. homomorphism 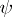 such that
such that 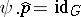 , has the property
, has the property
 |
where 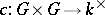 is a
is a  -cocycle of
-cocycle of 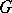 . The cohomology class of this cocycle is independent of the choice of the section
. The cohomology class of this cocycle is independent of the choice of the section  . It is determined by the projective representation
. It is determined by the projective representation 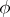 and determines the equivalence class of the extension (*). The condition
and determines the equivalence class of the extension (*). The condition 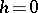 is necessary and sufficient for the projective representation
is necessary and sufficient for the projective representation 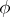 to be the composition of a linear representation of
to be the composition of a linear representation of 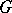 with the projection
with the projection 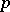 .
.
Projective representations arise naturally in studying linear representations of group extensions. The most important examples of projective representations are: the spinor representation of an orthogonal group and the Weyl representation of a symplectic group. The definitions of equivalence and irreducibility of representations carry over directly to projective representations. The classification of the irreducible projective representations of finite groups was obtained by I. Schur (1904).
A projective representation is said to be unitary if  is a Hilbert space and if the mapping
is a Hilbert space and if the mapping 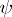 can be chosen so that it takes values in the group
can be chosen so that it takes values in the group 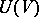 of unitary operators on
of unitary operators on 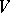 . Irreducible unitary projective representations of topological groups have been studied [4]; for a connected Lie group
. Irreducible unitary projective representations of topological groups have been studied [4]; for a connected Lie group 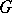 this study reduces to a study of the irreducible unitary representations of a simply-connected Lie group
this study reduces to a study of the irreducible unitary representations of a simply-connected Lie group  , the Lie algebra of which is the central extension of the Lie algebra
, the Lie algebra of which is the central extension of the Lie algebra 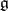 of the group
of the group 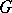 by a
by a 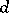 -dimensional commutative Lie algebra, where
-dimensional commutative Lie algebra, where 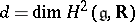 .
.
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
| [3] | G.W. Mackey, "Unitary representations of group extensions, I" Acta Math. , 99 (1958) pp. 265–311 |
| [4] | V. Bargmann, "Irreducible unitary representations of the Lorentz group" Ann. of Math. , 48 (1947) pp. 568–640 |
Comments
References
| [a1] | C.W. Curtis, I. Reiner, "Methods of representation theory" , 1–2 , Wiley (Interscience) (1981–1987) |
| [a2] | I.M. Isaacs, "Character theory of finite groups" , Acad. Press (1976) |
Projective representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_representation&oldid=49379