Difference between revisions of "Principal G-object"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48287 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''in a category'' | ''in a category'' | ||
| − | A concept in the theory of categories, instances of which are a [[Principal fibre bundle|principal fibre bundle]] in topology, a [[Principal homogeneous space|principal homogeneous space]] in algebraic geometry, etc. Let | + | A concept in the theory of categories, instances of which are a [[Principal fibre bundle|principal fibre bundle]] in topology, a [[Principal homogeneous space|principal homogeneous space]] in algebraic geometry, etc. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p0747103.png" /> be a [[Group object|group object]] in a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p0747104.png" /> with products and final object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p0747105.png" />. An object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p0747106.png" /> is said to be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p0747107.png" />-object if there is given a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p0747108.png" /> for which the following diagrams are commutative: |
| − | be a [[Group object|group object]] in a category | ||
| − | with products and final object | ||
| − | An object | ||
| − | is said to be a | ||
| − | object if there is given a morphism | ||
| − | for which the following diagrams are commutative: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p0747109.png" /></td> </tr></table> | |
| − | Here | + | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471010.png" /> is the group law morphism on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471011.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471012.png" /> is the unit element morphism into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471013.png" />. More precisely, the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471014.png" />-objects specified as above are called right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471016.png" />-objects; the definition of left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471018.png" />-objects is similar. As an example of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471019.png" />-object one may take the group object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471020.png" /> itself, for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471021.png" /> coincides with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471022.png" />. This object is called the trivial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471024.png" />-object. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471025.png" />-objects in the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471026.png" /> form a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471027.png" />. The morphisms are morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471028.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471029.png" /> which commute with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471030.png" /> (i.e. such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471031.png" />). A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471032.png" />-object is said to be a formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471034.png" />-object if the morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471035.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471036.png" /> induce an isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471037.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471038.png" /> is some [[Grothendieck topology|Grothendieck topology]] on the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471039.png" />, a formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471040.png" />-object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471041.png" /> is called a principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471042.png" />-object (with respect to the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471043.png" />) if there exists a covering <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471044.png" /> of the final object such that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471045.png" /> the product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471046.png" /> is isomorphic to the trivial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471047.png" />-object. |
| − | is the group law morphism on | ||
| − | while | ||
| − | is the unit element morphism into | ||
| − | More precisely, the | ||
| − | objects specified as above are called right | ||
| − | objects; the definition of left | ||
| − | objects is similar. As an example of a | ||
| − | object one may take the group object | ||
| − | itself, for which | ||
| − | coincides with | ||
| − | This object is called the trivial | ||
| − | object. The | ||
| − | objects in the category | ||
| − | form a category | ||
| − | The morphisms are morphism | ||
| − | of | ||
| − | which commute with | ||
| − | i.e. such that | ||
| − | A | ||
| − | object is said to be a formal principal | ||
| − | object if the morphisms | ||
| − | and | ||
| − | induce an isomorphism | ||
| − | If | ||
| − | is some [[Grothendieck topology|Grothendieck topology]] on the category | ||
| − | a formal principal | ||
| − | object | ||
| − | is called a principal | ||
| − | object (with respect to the topology | ||
| − | if there exists a covering | ||
| − | of the final object such that for any | ||
| − | the product | ||
| − | is isomorphic to the trivial | ||
| − | object. | ||
===Examples.=== | ===Examples.=== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 1) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471048.png" /> is the category of sets and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471049.png" /> is a group, then the non-empty <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471050.png" />-objects are called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471051.png" />-sets. These are sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471052.png" /> for which a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471053.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471054.png" />) is defined such that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471055.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471056.png" />, and for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471057.png" /> it is true that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471058.png" />. A principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471059.png" />-object is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471060.png" />-set in which for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471061.png" /> there exists a unique element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471062.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471063.png" /> (a principal homogeneous <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471065.png" />-set). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471066.png" /> is not empty, the choice of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471067.png" /> determines a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471068.png" /> which establishes an isomorphism between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471069.png" /> and the trivial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471070.png" />-set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471071.png" />. Thus, in any topology a formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471072.png" />-object is a principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471073.png" />-object. | |
| − | is | ||
| − | is a | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | If | + | 2) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471074.png" /> is a differentiable manifold and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471075.png" /> is a Lie group, then, taking <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471076.png" /> to be the category of fibrations over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471077.png" />, taking as group object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471078.png" /> the projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471079.png" />, and defining a topology in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471080.png" /> with the aid of families of open coverings, it is possible to obtain the definition of a principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471081.png" />-fibration. |
| − | is a | ||
| − | |||
| − | then | ||
| − | |||
| − | the | ||
| − | |||
| − | |||
| − | A formal principal | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471082.png" /> is a formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471083.png" />-object in a category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471084.png" />, then for any object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471085.png" /> in the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471086.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471087.png" /> is either empty or is a principal homogeneous <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471088.png" />-set. |
| − | object | + | |
| − | is isomorphic to the trivial | + | A formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471089.png" />-object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471090.png" /> is isomorphic to the trivial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471091.png" />-object if and only if there exists a section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471092.png" />. The set of isomorphism classes of formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471093.png" />-objects is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471094.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471095.png" /> is an Abelian group object, then the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471096.png" />, with the class of trivial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471097.png" />-objects as a base point, is a group and can be computed by standard tools of homological algebra. In general, in the computation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471098.png" /> Čech homology constructions are employed (cf. [[Non-Abelian cohomology|Non-Abelian cohomology]]). |
| − | object if and only if there exists a section | ||
| − | The set of isomorphism classes of formal principal | ||
| − | objects is denoted by | ||
| − | If | ||
| − | is an Abelian group object, then the set | ||
| − | with the class of trivial | ||
| − | objects as a base point, is a group and can be computed by standard tools of homological algebra. In general, in the computation of | ||
| − | Čech homology constructions are employed (cf. [[Non-Abelian cohomology|Non-Abelian cohomology]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck (ed.) et al. (ed.) , ''Revêtements étales et groupe fondamental. SGA 1'' , ''Lect. notes in math.'' , '''224''' , Springer (1971) {{MR|0354651}} {{ZBL|1039.14001}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck (ed.) et al. (ed.) , ''Revêtements étales et groupe fondamental. SGA 1'' , ''Lect. notes in math.'' , '''224''' , Springer (1971) {{MR|0354651}} {{ZBL|1039.14001}} </TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | Formal principal | + | Formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p07471099.png" />-objects are commonly called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p074710101.png" />-torsors. The distinction between formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p074710102.png" />-objects and principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p074710103.png" />-objects is not a profound one: a necessary and sufficient condition for a formal principal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p074710104.png" />-object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p074710105.png" /> to be principal is that the unique morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p074710106.png" /> should form a covering of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074710/p074710107.png" />. |
| − | objects are commonly called | ||
| − | torsors. The distinction between formal principal | ||
| − | objects and principal | ||
| − | objects is not a profound one: a necessary and sufficient condition for a formal principal | ||
| − | object | ||
| − | to be principal is that the unique morphism | ||
| − | should form a covering of | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Giraud, "Cohomologie non abélienne" , Springer (1971) {{MR|0344253}} {{ZBL|0226.14011}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Giraud, "Cohomologie non abélienne" , Springer (1971) {{MR|0344253}} {{ZBL|0226.14011}} </TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
in a category
A concept in the theory of categories, instances of which are a principal fibre bundle in topology, a principal homogeneous space in algebraic geometry, etc. Let 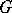 be a group object in a category
be a group object in a category 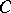 with products and final object
with products and final object  . An object
. An object 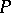 is said to be a
is said to be a 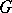 -object if there is given a morphism
-object if there is given a morphism  for which the following diagrams are commutative:
for which the following diagrams are commutative:
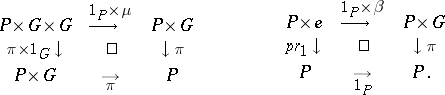 |
Here  is the group law morphism on
is the group law morphism on 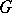 , while
, while 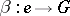 is the unit element morphism into
is the unit element morphism into 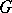 . More precisely, the
. More precisely, the 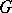 -objects specified as above are called right
-objects specified as above are called right 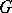 -objects; the definition of left
-objects; the definition of left 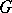 -objects is similar. As an example of a
-objects is similar. As an example of a 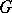 -object one may take the group object
-object one may take the group object 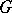 itself, for which
itself, for which 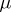 coincides with
coincides with 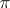 . This object is called the trivial
. This object is called the trivial 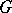 -object. The
-object. The 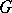 -objects in the category
-objects in the category 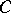 form a category
form a category 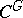 . The morphisms are morphism
. The morphisms are morphism  of
of 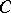 which commute with
which commute with 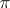 (i.e. such that
(i.e. such that 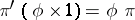 ). A
). A 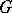 -object is said to be a formal principal
-object is said to be a formal principal  -object if the morphisms
-object if the morphisms  and
and 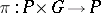 induce an isomorphism
induce an isomorphism 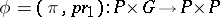 . If
. If 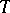 is some Grothendieck topology on the category
is some Grothendieck topology on the category 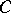 , a formal principal
, a formal principal 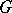 -object
-object 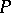 is called a principal
is called a principal 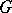 -object (with respect to the topology
-object (with respect to the topology 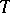 ) if there exists a covering
) if there exists a covering 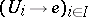 of the final object such that for any
of the final object such that for any 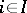 the product
the product 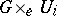 is isomorphic to the trivial
is isomorphic to the trivial 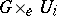 -object.
-object.
Examples.
1) If 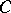 is the category of sets and
is the category of sets and 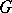 is a group, then the non-empty
is a group, then the non-empty 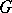 -objects are called
-objects are called 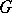 -sets. These are sets
-sets. These are sets 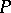 for which a mapping
for which a mapping 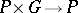 (
(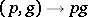 ) is defined such that for any
) is defined such that for any 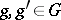 one has
one has 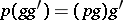 , and for any
, and for any 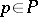 it is true that
it is true that  . A principal
. A principal 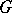 -object is a
-object is a 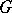 -set in which for any
-set in which for any 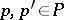 there exists a unique element
there exists a unique element 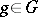 such that
such that 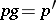 (a principal homogeneous
(a principal homogeneous 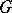 -set). If
-set). If 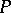 is not empty, the choice of a
is not empty, the choice of a 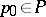 determines a mapping
determines a mapping 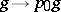 which establishes an isomorphism between
which establishes an isomorphism between 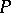 and the trivial
and the trivial 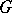 -set
-set 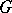 . Thus, in any topology a formal principal
. Thus, in any topology a formal principal 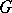 -object is a principal
-object is a principal 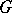 -object.
-object.
2) If 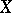 is a differentiable manifold and
is a differentiable manifold and 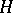 is a Lie group, then, taking
is a Lie group, then, taking 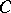 to be the category of fibrations over
to be the category of fibrations over 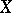 , taking as group object
, taking as group object 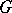 the projection
the projection 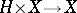 , and defining a topology in
, and defining a topology in 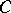 with the aid of families of open coverings, it is possible to obtain the definition of a principal
with the aid of families of open coverings, it is possible to obtain the definition of a principal 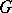 -fibration.
-fibration.
If 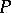 is a formal principal
is a formal principal 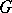 -object in a category
-object in a category 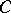 , then for any object
, then for any object 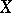 in the category
in the category 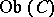 the set
the set 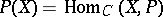 is either empty or is a principal homogeneous
is either empty or is a principal homogeneous 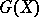 -set.
-set.
A formal principal 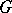 -object
-object 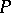 is isomorphic to the trivial
is isomorphic to the trivial 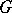 -object if and only if there exists a section
-object if and only if there exists a section 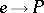 . The set of isomorphism classes of formal principal
. The set of isomorphism classes of formal principal 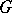 -objects is denoted by
-objects is denoted by 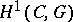 . If
. If 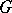 is an Abelian group object, then the set
is an Abelian group object, then the set 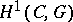 , with the class of trivial
, with the class of trivial  -objects as a base point, is a group and can be computed by standard tools of homological algebra. In general, in the computation of
-objects as a base point, is a group and can be computed by standard tools of homological algebra. In general, in the computation of 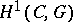 Čech homology constructions are employed (cf. Non-Abelian cohomology).
Čech homology constructions are employed (cf. Non-Abelian cohomology).
References
| [1] | A. Grothendieck (ed.) et al. (ed.) , Revêtements étales et groupe fondamental. SGA 1 , Lect. notes in math. , 224 , Springer (1971) MR0354651 Zbl 1039.14001 |
Comments
Formal principal 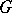 -objects are commonly called
-objects are commonly called 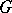 -torsors. The distinction between formal principal
-torsors. The distinction between formal principal 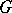 -objects and principal
-objects and principal 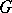 -objects is not a profound one: a necessary and sufficient condition for a formal principal
-objects is not a profound one: a necessary and sufficient condition for a formal principal 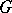 -object
-object 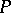 to be principal is that the unique morphism
to be principal is that the unique morphism 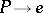 should form a covering of
should form a covering of  .
.
References
| [a1] | J. Giraud, "Cohomologie non abélienne" , Springer (1971) MR0344253 Zbl 0226.14011 |
Principal G-object. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Principal_G-object&oldid=49375