Difference between revisions of "Peirce decomposition"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48150 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | The representation of a ring as the direct sum of subrings related to a given idempotent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719701.png" />. For a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719702.png" /> containing an idempotent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719703.png" />, there exist left, right and two-sided Peirce decompositions, which are defined by |
| − | p0719701.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719704.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719705.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719706.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | respectively. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719707.png" /> has no identity, then one puts, by definition, | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719708.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p0719709.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197010.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | The sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197012.png" /> are defined analogously. Therefore, in a two-sided Peirce decomposition an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197013.png" /> can be represented as | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197014.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
in a left decomposition as | in a left decomposition as | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197015.png" /></td> </tr></table> | |
| − | |||
| − | |||
and in a right decomposition as | and in a right decomposition as | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197016.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | There is also a Peirce decomposition with respect to an orthogonal system of idempotents | + | There is also a Peirce decomposition with respect to an orthogonal system of idempotents <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197017.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197018.png" />: |
| − | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197019.png" /></td> </tr></table> | |
| − | |||
| − | |||
This decomposition was proposed by B. Peirce [[#References|[1]]]. | This decomposition was proposed by B. Peirce [[#References|[1]]]. | ||
| Line 76: | Line 35: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Peirce, "Linear associative algebra" ''Amer. J. Math.'' , '''4''' (1881) pp. 97–229</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Peirce, "Linear associative algebra" ''Amer. J. Math.'' , '''4''' (1881) pp. 97–229</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | In modern ring theory the Peirce decomposition appears in the ring of a Morita context | + | In modern ring theory the Peirce decomposition appears in the ring of a Morita context <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197020.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197022.png" /> are Morita related if they are subrings of a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197023.png" /> with an idempotent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197024.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197026.png" />, i.e., they are parts of a Peirce decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197027.png" /> (see [[#References|[a3]]], p.12). |
| − | where | ||
| − | and | ||
| − | are Morita related if they are subrings of a ring | ||
| − | with an idempotent | ||
| − | such that | ||
| − | |||
| − | i.e., they are parts of a Peirce decomposition of | ||
| − | see [[#References|[a3]]], p.12). | ||
| − | A context or a set of pre-equivalence data is a sextuple | + | A context or a set of pre-equivalence data is a sextuple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197028.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197030.png" /> are rings, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197031.png" /> is a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197032.png" />-, right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197033.png" />-bimodule, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197034.png" /> is a right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197035.png" />-, left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197036.png" />-bimodule and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197038.png" /> are bimodule homomorphisms, such that the following two associativity diagrams commute: |
| − | where | ||
| − | and | ||
| − | are rings, | ||
| − | is a left | ||
| − | right | ||
| − | bimodule, | ||
| − | is a right | ||
| − | left | ||
| − | bimodule and | ||
| − | |||
| − | are bimodule homomorphisms, such that the following two associativity diagrams commute: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197039.png" /></td> </tr></table> | |
and | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197040.png" /></td> </tr></table> | |
| − | Using | + | Using <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197041.png" />, the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197042.png" />-matrices |
| − | the set of all | ||
| − | matrices | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197043.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197044.png" /></td> </tr></table> | |
| − | = | ||
| − | |||
acquires a multiplication (using the usual matrix formulas) and this multiplication is associative precisely if the two diagrams above commute. Such a ring is then called the ring of a Morita context. | acquires a multiplication (using the usual matrix formulas) and this multiplication is associative precisely if the two diagrams above commute. Such a ring is then called the ring of a Morita context. | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197045.png" /> is a Morita context with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197046.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197047.png" /> epic, then the functors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197048.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197049.png" /> define an equivalence of categories between the categories of left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197050.png" />-modules and right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071970/p07197051.png" />-modules; cf. also [[Morita equivalence|Morita equivalence]]. Cf. [[#References|[a1]]], §4.1 for more details. |
| − | is a Morita context with | ||
| − | and | ||
| − | epic, then the functors | ||
| − | |||
| − | define an equivalence of categories between the categories of left | ||
| − | modules and right | ||
| − | modules; cf. also [[Morita equivalence|Morita equivalence]]. Cf. [[#References|[a1]]], §4.1 for more details. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.H. Rowen, "Ring theory" , '''I''' , Acad. Press (1988) pp. 36</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) pp. 48, 50</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.H. Rowen, "Ring theory" , '''I''' , Acad. Press (1988) pp. 36</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) pp. 48, 50</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987)</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
The representation of a ring as the direct sum of subrings related to a given idempotent  . For a ring
. For a ring  containing an idempotent
containing an idempotent  , there exist left, right and two-sided Peirce decompositions, which are defined by
, there exist left, right and two-sided Peirce decompositions, which are defined by
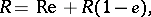 |
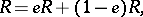 |
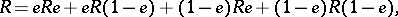 |
respectively. If  has no identity, then one puts, by definition,
has no identity, then one puts, by definition,
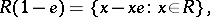 |
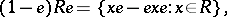 |
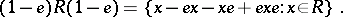 |
The sets 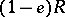 and
and 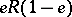 are defined analogously. Therefore, in a two-sided Peirce decomposition an element
are defined analogously. Therefore, in a two-sided Peirce decomposition an element 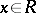 can be represented as
can be represented as
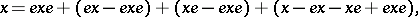 |
in a left decomposition as
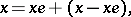 |
and in a right decomposition as
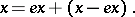 |
There is also a Peirce decomposition with respect to an orthogonal system of idempotents 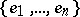 where
where 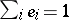 :
:
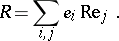 |
This decomposition was proposed by B. Peirce [1].
References
| [1] | B. Peirce, "Linear associative algebra" Amer. J. Math. , 4 (1881) pp. 97–229 |
Comments
In modern ring theory the Peirce decomposition appears in the ring of a Morita context 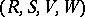 , where
, where  and
and 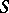 are Morita related if they are subrings of a ring
are Morita related if they are subrings of a ring  with an idempotent
with an idempotent  such that
such that 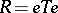 ,
, 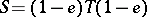 , i.e., they are parts of a Peirce decomposition of
, i.e., they are parts of a Peirce decomposition of 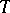 (see [a3], p.12).
(see [a3], p.12).
A context or a set of pre-equivalence data is a sextuple  where
where 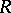 and
and  are rings,
are rings, 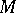 is a left
is a left  -, right
-, right 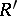 -bimodule,
-bimodule,  is a right
is a right 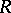 -, left
-, left 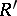 -bimodule and
-bimodule and 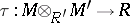 ,
, 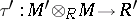 are bimodule homomorphisms, such that the following two associativity diagrams commute:
are bimodule homomorphisms, such that the following two associativity diagrams commute:
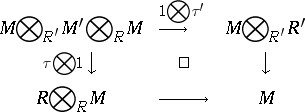 |
and
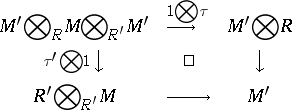 |
Using  , the set of all
, the set of all 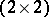 -matrices
-matrices
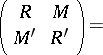 |
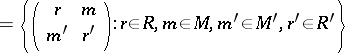 |
acquires a multiplication (using the usual matrix formulas) and this multiplication is associative precisely if the two diagrams above commute. Such a ring is then called the ring of a Morita context.
If  is a Morita context with
is a Morita context with  and
and 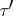 epic, then the functors
epic, then the functors 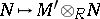 ,
, 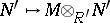 define an equivalence of categories between the categories of left
define an equivalence of categories between the categories of left  -modules and right
-modules and right  -modules; cf. also Morita equivalence. Cf. [a1], §4.1 for more details.
-modules; cf. also Morita equivalence. Cf. [a1], §4.1 for more details.
References
| [a1] | L.H. Rowen, "Ring theory" , I , Acad. Press (1988) pp. 36 |
| [a2] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) pp. 48, 50 |
| [a3] | J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) |
Peirce decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Peirce_decomposition&oldid=49362