Difference between revisions of "Meijer-G-functions"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47819 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | Generalizations of the hypergeometric functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101102.png" /> of one variable (cf. also [[Hypergeometric function|Hypergeometric function]]). They can be defined by an integral as |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101103.png" /></td> </tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101104.png" /></td> </tr></table> | |
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101105.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101106.png" /> and the parameters <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101107.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101108.png" /> are such that no pole of the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m1101109.png" /> coincides with any pole of the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011010.png" />. There are three possible choices for the contour <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011011.png" />: | |
| − | |||
| − | + | a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011012.png" /> goes from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011013.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011014.png" /> remaining to the right of the poles of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011015.png" /> and to the left of the poles of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011016.png" />; | |
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011017.png" /> begins and ends at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011018.png" />, encircles counterclockwise all poles of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011019.png" /> and does not encircle any pole of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011020.png" />; | |
| − | |||
| − | and | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | c) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011021.png" /> begins and ends at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011022.png" />, encircles clockwise all poles of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011023.png" /> and does not encircle any pole of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011024.png" />. | |
| − | |||
| − | |||
| − | |||
| − | and | ||
| − | + | The integral converges if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011026.png" /> in case a); if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011027.png" /> and either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011028.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011030.png" /> in case b); and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011031.png" /> and either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011032.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011033.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011034.png" /> in case c). | |
| − | |||
| − | |||
| − | and | ||
| − | + | The integral defining the Meijer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011035.png" />-functions can be calculated by means of the residue theorem and one obtains expressions for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011036.png" /> in terms of the hypergeometric functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011037.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011038.png" />. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011039.png" /> satisfies the linear differential equation | |
| − | |||
| − | |||
| − | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011040.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011041.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011042.png" /></td> </tr></table> | |
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Many functions of hypergeometric type and their products can be expressed in terms of Meijer | + | Many functions of hypergeometric type and their products can be expressed in terms of Meijer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011043.png" />-functions, [[#References|[a1]]]. For example, |
| − | functions, [[#References|[a1]]]. For example, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011044.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011045.png" /></td> </tr></table> | |
| − | |||
| − | Meijer | + | Meijer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m110/m110110/m11011046.png" />-functions appear in the theory of [[Lie group|Lie group]] representations (cf. also [[Representation of a compact group|Representation of a compact group]]) as transition coefficients for different bases of carrier spaces of representations [[#References|[a2]]]. |
| − | functions appear in the theory of [[Lie group|Lie group]] representations (cf. also [[Representation of a compact group|Representation of a compact group]]) as transition coefficients for different bases of carrier spaces of representations [[#References|[a2]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Erdelyi, W. Magnus, F. Oberhettinger, F. Tricomi, "Higher transcendental functions" , '''1''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.J. Vilenkin, A.U. Klimyk, "Representation of Lie groups and special functions" , '''2''' , Kluwer Acad. Publ. (1993) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Erdelyi, W. Magnus, F. Oberhettinger, F. Tricomi, "Higher transcendental functions" , '''1''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.J. Vilenkin, A.U. Klimyk, "Representation of Lie groups and special functions" , '''2''' , Kluwer Acad. Publ. (1993) (In Russian)</TD></TR></table> | ||
Revision as of 10:26, 7 June 2020
Generalizations of the hypergeometric functions 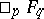 of one variable (cf. also Hypergeometric function). They can be defined by an integral as
of one variable (cf. also Hypergeometric function). They can be defined by an integral as
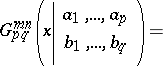 |
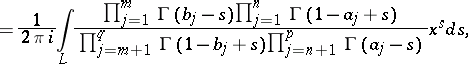 |
where  ,
, 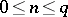 and the parameters
and the parameters 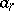 ,
, 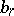 are such that no pole of the functions
are such that no pole of the functions 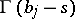 coincides with any pole of the functions
coincides with any pole of the functions 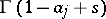 . There are three possible choices for the contour
. There are three possible choices for the contour 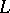 :
:
a) 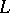 goes from
goes from 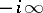 to
to  remaining to the right of the poles of
remaining to the right of the poles of 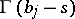 and to the left of the poles of
and to the left of the poles of 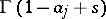 ;
;
b) 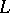 begins and ends at
begins and ends at 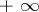 , encircles counterclockwise all poles of
, encircles counterclockwise all poles of 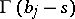 and does not encircle any pole of
and does not encircle any pole of 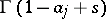 ;
;
c) 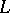 begins and ends at
begins and ends at 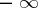 , encircles clockwise all poles of
, encircles clockwise all poles of 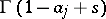 and does not encircle any pole of
and does not encircle any pole of 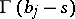 .
.
The integral converges if 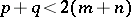 ,
, 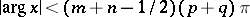 in case a); if
in case a); if 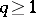 and either
and either 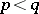 or
or  and
and  in case b); and if
in case b); and if 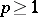 and either
and either 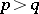 or
or  and
and 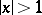 in case c).
in case c).
The integral defining the Meijer 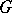 -functions can be calculated by means of the residue theorem and one obtains expressions for
-functions can be calculated by means of the residue theorem and one obtains expressions for 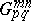 in terms of the hypergeometric functions
in terms of the hypergeometric functions 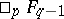 or
or 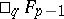 . The function
. The function 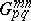 satisfies the linear differential equation
satisfies the linear differential equation
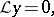 |
where
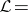 |
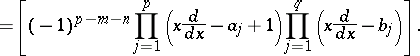 |
Many functions of hypergeometric type and their products can be expressed in terms of Meijer 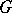 -functions, [a1]. For example,
-functions, [a1]. For example,
 |
 |
Meijer  -functions appear in the theory of Lie group representations (cf. also Representation of a compact group) as transition coefficients for different bases of carrier spaces of representations [a2].
-functions appear in the theory of Lie group representations (cf. also Representation of a compact group) as transition coefficients for different bases of carrier spaces of representations [a2].
References
| [a1] | A. Erdelyi, W. Magnus, F. Oberhettinger, F. Tricomi, "Higher transcendental functions" , 1 , McGraw-Hill (1953) |
| [a2] | N.J. Vilenkin, A.U. Klimyk, "Representation of Lie groups and special functions" , 2 , Kluwer Acad. Publ. (1993) (In Russian) |
Meijer-G-functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Meijer-G-functions&oldid=49295