Difference between revisions of "User:Maximilian Janisch/Sandbox"
(Automatic edit) |
(copy of fourier transform article) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|part}} | |
| + | |||
| + | One of the integral transforms (cf. [[Integral transform|Integral transform]]). It is a linear operator $F$ acting on a space whose elements are functions $f$ of $n$ real variables. The smallest domain of definition of $F$ is the set $D=C_0^\infty$ of all infinitely-differentiable functions $\phi$ of compact support. For such functions | ||
| + | |||
| + | \begin{equation} (F\phi)(x) = \frac{1}{(2\pi)^{\frac{n}{2}}} \cdot \int_{\mathbf R^n} \phi(\xi) e^{-i x \xi} \, \mathrm d\xi. \end{equation} | ||
| + | |||
| + | In a certain sense the most natural domain of definition of $F$ is the set $S$ of all infinitely-differentiable functions $\phi$ that, together with their derivatives, vanish at infinity faster than any power of $\frac{1}{|x|}$. Formula (1) still holds for $\phi\in S$, and $(F \phi)(x) \equiv \psi(x)\in S$. Moreover, $F$ is an isomorphism of $S$ <u>onto</u> itself, the inverse mapping $F^{-1}$ (the inverse Fourier transform) is the inverse of the Fourier transform and is given by the formula: | ||
| + | |||
| + | \begin{equation} \phi(x) = (F^{-1} \psi)(x) = \frac{1}{(2\pi)^{\frac{n}{2}}} \cdot \int_{\mathbf R^n} \psi(\xi) e^{i x \xi} \, \mathrm d\xi. \end{equation} | ||
| + | |||
| + | Formula (1) also acts on the space $L_{1}\left(\mathbf{R}^{n}\right)$ of integrable functions. In order to enlarge the domain of definition of the operator $F$ generalization of (1) is necessary. In classical analysis such a generalization has been constructed for locally integrable functions with some restriction on their behaviour as $|x|\to\infty$ (see [[Fourier integral|Fourier integral]]). In the theory of generalized functions the definition of the operator $F$ is free of many requirements of classical analysis. | ||
| + | |||
| + | The basic problems connected with the study of the Fourier transform $F$ are: the investigation of the domain of definition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115023.png" /> and the range of values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115024.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115025.png" />; as well as studying properties of the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115026.png" /> (in particular, conditions for the existence of the inverse operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115027.png" /> and its expression). The inversion formula for the Fourier transform is very simple: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115028.png" /></td> </tr></table> | ||
| + | |||
| + | Under the action of the Fourier transform linear operators on the original space, which are invariant with respect to a shift, become (under certain conditions) multiplication operators in the image space. In particular, the convolution of two functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115030.png" /> goes over into the product of the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115032.png" />: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115033.png" /></td> </tr></table> | ||
| + | |||
| + | and differentiation induces multiplication by the independent variable: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115034.png" /></td> </tr></table> | ||
| + | |||
| + | In the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115036.png" />, the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115037.png" /> is defined by the formula (1) on the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115038.png" /> and is a bounded operator from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115039.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115040.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115041.png" />: | ||
| + | |||
| + | \begin{equation} \left\{\frac{1}{(2 \pi)^{n / 2}} \int_{\mathbf{R}^{n}}|(F f)(x)|^{q} d x\right\}^{1 / q} \leq\left\{\frac{1}{(2 \pi)^{n / 2}} \int_{\mathbf{R}^{n}}|f(x)|^{p} d x\right\}^{1 / p} \end{equation} | ||
| + | |||
| + | (the Hausdorff–Young inequality). <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115043.png" /> admits a continuous extension onto the whole space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115044.png" /> which (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115045.png" />) is given by | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115046.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | ||
| + | |||
| + | Convergence is understood to be in the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115047.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115048.png" />, the image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115049.png" /> under the action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115050.png" /> does not coincide with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115051.png" />, that is, the imbedding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115052.png" /> is strict when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115053.png" /> (for the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115054.png" /> see [[Plancherel theorem|Plancherel theorem]]). The inverse operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115055.png" /> is defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115056.png" /> by | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115057.png" /></td> </tr></table> | ||
| + | |||
| + | The problem of extending the Fourier transform to a larger class of functions arises constantly in analysis and its applications. See, for example, [[Fourier transform of a generalized function|Fourier transform of a generalized function]]. | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Zygmund, "Trigonometric series" , '''2''' , Cambridge Univ. Press (1988)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.M. Stein, G. Weiss, "Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971)</TD></TR></table> | ||
| + | |||
| + | |||
| + | |||
| + | ====Comments==== | ||
| + | Instead of "generalized function" the term "distributiondistribution" is often used. | ||
| + | |||
| + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115058.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115059.png" /> then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115060.png" /> denotes the scalar product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115061.png" />. | ||
| + | |||
| + | If in (1) the "normalizing factor" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115062.png" /> is replaced by some constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115063.png" />, then in (2) it must be replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115064.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115065.png" />. | ||
| + | |||
| + | At least two other conventions for the "normalization factor" are in common use: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115066.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115067.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115068.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115069.png" /></td> </tr></table> | ||
| + | |||
| + | The convention of the article leads to the Fourier transform as a [[Unitary operator|unitary operator]] from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041150/f04115070.png" /> into itself, and so does the convention (a2). Convention (a1) is more in line with [[Harmonic analysis|harmonic analysis]]. | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Functional analysis" , McGraw-Hill (1973)</TD></TR></table> | ||
Revision as of 16:34, 6 April 2019
One of the integral transforms (cf. Integral transform). It is a linear operator $F$ acting on a space whose elements are functions $f$ of $n$ real variables. The smallest domain of definition of $F$ is the set $D=C_0^\infty$ of all infinitely-differentiable functions $\phi$ of compact support. For such functions
\begin{equation} (F\phi)(x) = \frac{1}{(2\pi)^{\frac{n}{2}}} \cdot \int_{\mathbf R^n} \phi(\xi) e^{-i x \xi} \, \mathrm d\xi. \end{equation}
In a certain sense the most natural domain of definition of $F$ is the set $S$ of all infinitely-differentiable functions $\phi$ that, together with their derivatives, vanish at infinity faster than any power of $\frac{1}{|x|}$. Formula (1) still holds for $\phi\in S$, and $(F \phi)(x) \equiv \psi(x)\in S$. Moreover, $F$ is an isomorphism of $S$ onto itself, the inverse mapping $F^{-1}$ (the inverse Fourier transform) is the inverse of the Fourier transform and is given by the formula:
\begin{equation} \phi(x) = (F^{-1} \psi)(x) = \frac{1}{(2\pi)^{\frac{n}{2}}} \cdot \int_{\mathbf R^n} \psi(\xi) e^{i x \xi} \, \mathrm d\xi. \end{equation}
Formula (1) also acts on the space $L_{1}\left(\mathbf{R}^{n}\right)$ of integrable functions. In order to enlarge the domain of definition of the operator $F$ generalization of (1) is necessary. In classical analysis such a generalization has been constructed for locally integrable functions with some restriction on their behaviour as $|x|\to\infty$ (see Fourier integral). In the theory of generalized functions the definition of the operator $F$ is free of many requirements of classical analysis.
The basic problems connected with the study of the Fourier transform $F$ are: the investigation of the domain of definition 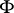 and the range of values
and the range of values 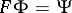 of
of 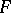 ; as well as studying properties of the mapping
; as well as studying properties of the mapping 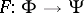 (in particular, conditions for the existence of the inverse operator
(in particular, conditions for the existence of the inverse operator 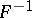 and its expression). The inversion formula for the Fourier transform is very simple:
and its expression). The inversion formula for the Fourier transform is very simple:
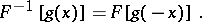 |
Under the action of the Fourier transform linear operators on the original space, which are invariant with respect to a shift, become (under certain conditions) multiplication operators in the image space. In particular, the convolution of two functions 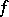 and
and 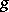 goes over into the product of the functions
goes over into the product of the functions  and
and 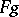 :
:
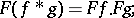 |
and differentiation induces multiplication by the independent variable:
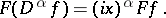 |
In the spaces 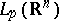 ,
, 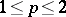 , the operator
, the operator 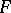 is defined by the formula (1) on the set
is defined by the formula (1) on the set 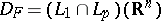 and is a bounded operator from
and is a bounded operator from 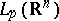 into
into 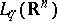 ,
, 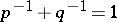 :
:
\begin{equation} \left\{\frac{1}{(2 \pi)^{n / 2}} \int_{\mathbf{R}^{n}}|(F f)(x)|^{q} d x\right\}^{1 / q} \leq\left\{\frac{1}{(2 \pi)^{n / 2}} \int_{\mathbf{R}^{n}}|f(x)|^{p} d x\right\}^{1 / p} \end{equation}
(the Hausdorff–Young inequality).  admits a continuous extension onto the whole space
admits a continuous extension onto the whole space 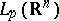 which (for
which (for 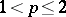 ) is given by
) is given by
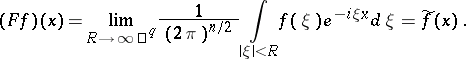 | (3) |
Convergence is understood to be in the norm of 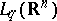 . If
. If 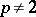 , the image of
, the image of 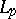 under the action of
under the action of 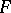 does not coincide with
does not coincide with 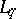 , that is, the imbedding
, that is, the imbedding 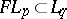 is strict when
is strict when 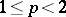 (for the case
(for the case 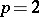 see Plancherel theorem). The inverse operator
see Plancherel theorem). The inverse operator 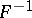 is defined on
is defined on 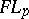 by
by
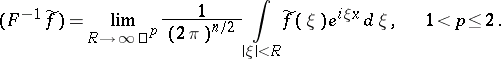 |
The problem of extending the Fourier transform to a larger class of functions arises constantly in analysis and its applications. See, for example, Fourier transform of a generalized function.
References
| [1] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
| [2] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
| [3] | E.M. Stein, G. Weiss, "Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Comments
Instead of "generalized function" the term "distributiondistribution" is often used.
If 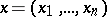 and
and 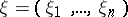 then
then  denotes the scalar product
denotes the scalar product 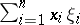 .
.
If in (1) the "normalizing factor" 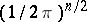 is replaced by some constant
is replaced by some constant  , then in (2) it must be replaced by
, then in (2) it must be replaced by 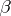 with
with 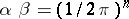 .
.
At least two other conventions for the "normalization factor" are in common use:
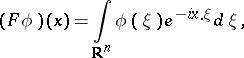 | (a1) |
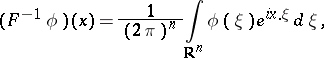 |
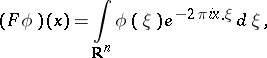 | (a2) |
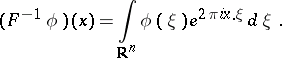 |
The convention of the article leads to the Fourier transform as a unitary operator from  into itself, and so does the convention (a2). Convention (a1) is more in line with harmonic analysis.
into itself, and so does the convention (a2). Convention (a1) is more in line with harmonic analysis.
References
| [a1] | W. Rudin, "Functional analysis" , McGraw-Hill (1973) |
Maximilian Janisch/Sandbox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/Sandbox&oldid=43661