Wronskian

Wronski determinant

The determinant of a system of $n$ vector-functions of dimension $n$,

$$ \phi_i(t) = \{ \phi_i^1(t), \ldots , \phi_i^n(t) \}, \quad i = 1, \ldots, n \tag{1} \label{eq-1} $$

of the type

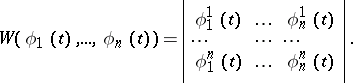The Wronskian of a system of scalar functions

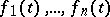(2)

which have derivatives up to order 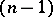(inclusive) is the determinant

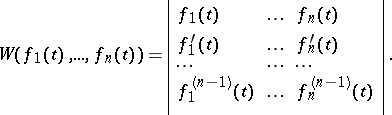(3)

The concept was first introduced by J. Wronski [1].

If the vector-functions (1) are linearly dependent on a set 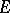, then

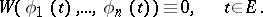If the scalar functions (2) are linearly dependent on a set , then

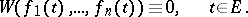The converse theorems are usually not true: Identical vanishing of a Wronskian on some set is not a sufficient condition for linear dependence of functions on this set.

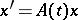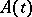Let the vector-functions (1) be the solutions of a linear homogeneous -th order system , , with an -dimensional matrix that is continuous on an interval 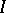. If these solutions constitute a fundamental system, then

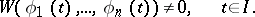If the Wronskian of these solutions is equal to zero in at least one point of 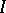, it is identically equal to zero on 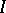, and the functions (1) are linearly dependent. The Liouville formula

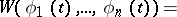where 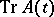is the trace of the matrix 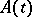, is applicable.

Let the functions (2) be the solutions of a linear homogeneous -th order equation

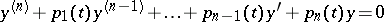with continuous coefficients on the interval 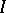. If these solutions constitute a fundamental system, then

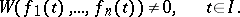If the Wronskian of these solutions is zero in at least one point of , it is identically equal to zero on 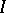, and the functions (2) are linearly dependent. The Liouville formula

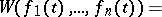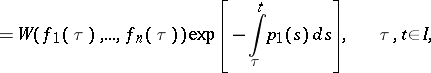applies.

References

[1]	J. Hoene-Wronski, "Réfutation de la théorie des fonctions analytiques de Lagrange" , Paris (1812)
[2]	L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian)

Comments

An example of functions (2) that are not linearly dependent but with vanishing Wronskian was given by G. Peano, [a3].

A sub-Wronskian of orde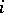r for 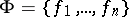is obtained by taking the Wronskian of a subset of size 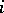of 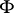. Two theorems giving sufficient conditions for linear dependence in terms of Wronskians are as follows. 1) Let 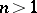, 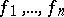analytic and 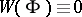, then the 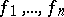are linearly dependent, [a4], [a5]. 2) Let , , 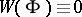but at no point of the interval of definition of 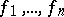do all sub-Wronskians of order 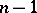vanish simultaneously, then 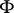is linearly dependent, [a3].

For more information and results concerning functions of several variables, cf. [a6], [a7].

References

[a1]	T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974)
[a2]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)
[a3]	G. Peano, "Sur le déterminant Wronskian" Mathesis , 9 (1889) pp. 75–76
[a4]	M. Böcher, "Certain cases in which the vanishing of the Wronskian is a sufficient condition for linear dependence" Trans. Amer. Math. Soc. , 2 (1901) pp. 139–149
[a5]	D.R. Curtis, "The vanishing of the Wronskian and the problem of linear dependence" Math. Ann. , 65 (1908) pp. 282–298
[a6]	K. Wolsson, "A condition equivalent to linear dependence for functions with vanishing Wronskian" Linear Alg. Appl. , 116 (1989) pp. 1–8
[a7]	K. Wolsson, "Linear dependence of a function set of variables with vanishing generalized Wronskians" Linear Alg. Appl. , 117 (1989) pp. 73–80