Difference between revisions of "Period of a function"
From Encyclopedia of Mathematics
(Importing text file) |
(continuity required (see talk)) |
||
| Line 9: | Line 9: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215014.png" /></td> </tr></table> | ||
| − | any rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215015.png" /> is a period. If a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215016.png" /> has period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215017.png" />, then the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215020.png" /> are constants and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215021.png" />, has period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215022.png" />. If a real-valued function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215023.png" /> of a real argument is periodic on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215024.png" /> (and is not identically equal to a constant), then it has a least period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215025.png" /> and any other real period is a multiple of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215026.png" />. There exist non-constant functions of a complex argument having two non-multiple periods with imaginary quotient, such as for example an [[Elliptic function|elliptic function]]. | + | any rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215015.png" /> is a period. If a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215016.png" /> has period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215017.png" />, then the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215020.png" /> are constants and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215021.png" />, has period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215022.png" />. If a real-valued function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215023.png" /> of a real argument is continuous and periodic on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215024.png" /> (and is not identically equal to a constant), then it has a least period <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215025.png" /> and any other real period is a multiple of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072150/p07215026.png" />. There exist non-constant functions of a complex argument having two non-multiple periods with imaginary quotient, such as for example an [[Elliptic function|elliptic function]]. |
Similarly one defines the period of a function defined on an Abelian group. | Similarly one defines the period of a function defined on an Abelian group. | ||
Revision as of 07:30, 21 October 2017
A number 
such that for any 
(or 
) the numbers 
and 
also belong to 
and such that the following equality holds:
 |
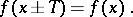The numbers 
, where 
is a natural number, are also periods of 
. For a function 
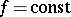on an axis or on a plane, any number 
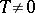is a period; for the Dirichlet function
 |
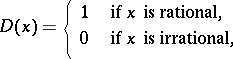any rational number 
is a period. If a function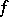 
has period 
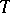, then the function 
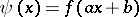, where 
and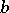 
are constants and 
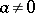, has period 
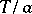. If a real-valued function 
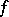of a real argument is continuous and periodic on 
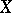(and is not identically equal to a constant), then it has a least period 
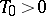and any other real period is a multiple of 
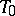. There exist non-constant functions of a complex argument having two non-multiple periods with imaginary quotient, such as for example an elliptic function.
Similarly one defines the period of a function defined on an Abelian group.
Comments
Cf. also Periodic function.
How to Cite This Entry:
Period of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Period_of_a_function&oldid=42145
Period of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Period_of_a_function&oldid=42145
This article was adapted from an original article by A.A. Konyushkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article