Difference between revisions of "Random field"
Ulf Rehmann (talk | contribs) m (→Refs) |
Ulf Rehmann (talk | contribs) m (Reverted edits by Ulf Rehmann (talk) to last revision by 127.0.0.1) |
||
| Line 1: | Line 1: | ||
| + | ''stochastic process in multi-dimensional time, stochastic process with a multi-dimensional parameter'' | ||
| − | + | A [[Random function|random function]] defined on a set of points in a multi-dimensional space. Random fields are an important example of random functions (cf. [[Random element|Random element]]), which are often encountered in various applications. Some examples of random fields depending on three spatial coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773001.png" /> (as well as on the time <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773002.png" />) are the fields of components of the velocity, of the pressure and of the temperature of a turbulent fluid flow (see [[#References|[1]]]). An example of a random field depending on two coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773003.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773004.png" /> is the height <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773005.png" /> of a wavy sea surface, or the surface of any rough plate (see [[#References|[2]]]). In the investigation of global atmospheric processes on an Earth scale, the field of ground pressure and other meteorological characteristics are sometimes regarded as random fields on a sphere, etc. | |
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | + | The theory of random fields of a general form is almost identical with the general theory of random functions. One can only obtain more interesting concrete results for various special classes of random fields with additional properties that facilitate their study. One such class is that of homogeneous random fields (cf. [[Random field, homogeneous|Random field, homogeneous]]), defined on a homogeneous space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773006.png" /> with a group of transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773007.png" /> and having the property that the probability distributions of the values of the field on an arbitrary finite group of points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773008.png" />, or the mean value of the field and the second moments of its values on pairs of points, are invariant under the action of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r0773009.png" /> on their arguments. Homogeneous random fields on a Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730011.png" /> or on the lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730012.png" /> of points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730013.png" /> with integral coordinates, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730014.png" /> is the group of all possible (or all integral) parallel translations, are natural generalizations of stationary stochastic processes (cf. [[Stationary stochastic process|Stationary stochastic process]]), and many results that hold for such processes carry over in a simple way. Of great interest for applications (in particular, for the mechanics of turbulence, see [[#References|[1]]]) are the so-called homogeneous isotropic random fields on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730016.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730017.png" /> is the group of isometric transformations of the corresponding space. An important feature of homogeneous random fields is the existence of a spectral decomposition of special form, both of the fields themselves and of their correlation functions (see, for example, [[#References|[3]]], [[#References|[4]]], ; see also [[Spectral decomposition of a random function|Spectral decomposition of a random function]]). | |
| + | Another class of random fields that has attracted considerable attention is that of Markov random fields, defined in some domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730018.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730019.png" />. The condition for a random field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730020.png" /> of being Markov asserts, roughly speaking, that for a sufficiently large family of open sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730021.png" /> with boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730022.png" />, fixing the values taken by the field in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730023.png" />-neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730024.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730025.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730026.png" /> gives that the families of random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730027.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730028.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730029.png" /> is the complement of the closure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730030.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730031.png" />, are mutually independent (or, in the case of the Markov property in the wide sense, mutually uncorrelated; see, for example, [[#References|[5]]]). This can be generalized to the concept of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730033.png" />-Markov random fields, where the above independence (or orthogonality) need only hold when the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730034.png" />-neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730035.png" /> of arbitrary width is replaced by a special type of thickened boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730036.png" />. The theory of Markov random fields and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730038.png" />-Markov fields has a number of important applications in quantum field theory and statistical physics (see [[#References|[6]]], [[#References|[7]]]). Another class of random fields arising from problems of statistical physics is that of Gibbs random fields, whose probability distributions can be expressed as Gibbs distributions (cf. [[Gibbs distribution|Gibbs distribution]]; see e.g. [[#References|[7]]], [[#References|[8]]], [[#References|[10]]]). A convenient way of defining Gibbs random fields involves a family of conditional probability distributions of values of the field in a finite domain corresponding to all its fixed values outside this domain. It must be noted that it is often convenient to regard random fields on a smooth manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730039.png" /> as a special case of generalized random fields, for which there may not exist values at one specified point, but the smoothened values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730040.png" /> can be interpreted as random linear functionals defined on some space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730041.png" /> of smooth test functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730042.png" />. Generalized random fields (and especially generalized Markov random fields) are widely used in physical applications. By considering within the limits of the theory of generalized random fields (cf. [[Random field, generalized|Random field, generalized]]) the fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730043.png" />, where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730044.png" /> are such that | ||
| − | < | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730045.png" /></td> </tr></table> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | it is also possible to define the concepts of the locally homogeneous (and locally homogeneous and locally isotropic) random fields related to stochastic processes with stationary increments (cf. [[Stochastic process with stationary increments|Stochastic process with stationary increments]]); see [[#References|[10]]], . Such fields play an important role in the statistical theory of turbulence (see, for example, [[#References|[1]]], [[#References|[9]]]). | ||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.S. Monin, A.M. Yaglom, "Statistical fluid mechanics" , '''1–2''' , M.I.T. (1971–1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.P. Khusu, Yu.R. Vitenberg, V.A. Pal'mov, "Surface roughness (a probabilistic approach)" , Moscow (1975) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.J. Hannan, "Group representations and applied probability" , Methuen (1965)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.I. Yadrenko, "Spectral theory of random fields" , Optim. Software (1983) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Yu.A. Rozanov, "Markov random fields" , Springer (1982) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077300/r07730046.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> K. Preston, "Gibbs states on countable sets" , Cambridge Univ. Press (1974)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , ''Multi-component random systems'' , M. Dekker (1980) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , '''4''' , Acad. Press (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.A. Malyshev, R.A. Minlos, "Gibbs random fields" , Kluwer (1990) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ====Comments==== | ||
| + | For Gibbs and Markov fields see also [[#References|[a2]]]–[[#References|[a3]]]. The estimation theory of random fields is discussed in [[#References|[a4]]]–[[#References|[a5]]]. For limit theorems concerning random fields cf. [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
| − | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Adler, "The geometry of random fields" , Wiley (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Non standard methods in stochastic analysis and mathematical physics" , Acad. Press (1986)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.-O. Georgii, "Gibbs measures and phase transitions" , de Gruyter (1988)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.G. Ramm, "Random fields: estimation theory" , Longman & Wiley (1990)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A.V. Ivanov, N.N. Leonenko, "Statistical analysis of random fields" , Kluwer (1989) (Translated from Russian)</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | < | ||
| − | |||
| − | |||
Revision as of 11:44, 3 April 2016
stochastic process in multi-dimensional time, stochastic process with a multi-dimensional parameter
A random function defined on a set of points in a multi-dimensional space. Random fields are an important example of random functions (cf. Random element), which are often encountered in various applications. Some examples of random fields depending on three spatial coordinates  (as well as on the time
(as well as on the time  ) are the fields of components of the velocity, of the pressure and of the temperature of a turbulent fluid flow (see [1]). An example of a random field depending on two coordinates
) are the fields of components of the velocity, of the pressure and of the temperature of a turbulent fluid flow (see [1]). An example of a random field depending on two coordinates  and
and  is the height
is the height  of a wavy sea surface, or the surface of any rough plate (see [2]). In the investigation of global atmospheric processes on an Earth scale, the field of ground pressure and other meteorological characteristics are sometimes regarded as random fields on a sphere, etc.
of a wavy sea surface, or the surface of any rough plate (see [2]). In the investigation of global atmospheric processes on an Earth scale, the field of ground pressure and other meteorological characteristics are sometimes regarded as random fields on a sphere, etc.
The theory of random fields of a general form is almost identical with the general theory of random functions. One can only obtain more interesting concrete results for various special classes of random fields with additional properties that facilitate their study. One such class is that of homogeneous random fields (cf. Random field, homogeneous), defined on a homogeneous space  with a group of transformations
with a group of transformations 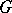 and having the property that the probability distributions of the values of the field on an arbitrary finite group of points of
and having the property that the probability distributions of the values of the field on an arbitrary finite group of points of  , or the mean value of the field and the second moments of its values on pairs of points, are invariant under the action of elements of
, or the mean value of the field and the second moments of its values on pairs of points, are invariant under the action of elements of  on their arguments. Homogeneous random fields on a Euclidean space
on their arguments. Homogeneous random fields on a Euclidean space 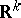 ,
,  or on the lattice
or on the lattice 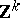 of points of
of points of 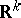 with integral coordinates, where
with integral coordinates, where  is the group of all possible (or all integral) parallel translations, are natural generalizations of stationary stochastic processes (cf. Stationary stochastic process), and many results that hold for such processes carry over in a simple way. Of great interest for applications (in particular, for the mechanics of turbulence, see [1]) are the so-called homogeneous isotropic random fields on
is the group of all possible (or all integral) parallel translations, are natural generalizations of stationary stochastic processes (cf. Stationary stochastic process), and many results that hold for such processes carry over in a simple way. Of great interest for applications (in particular, for the mechanics of turbulence, see [1]) are the so-called homogeneous isotropic random fields on  and
and 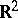 , where
, where  is the group of isometric transformations of the corresponding space. An important feature of homogeneous random fields is the existence of a spectral decomposition of special form, both of the fields themselves and of their correlation functions (see, for example, [3], [4], ; see also Spectral decomposition of a random function).
is the group of isometric transformations of the corresponding space. An important feature of homogeneous random fields is the existence of a spectral decomposition of special form, both of the fields themselves and of their correlation functions (see, for example, [3], [4], ; see also Spectral decomposition of a random function).
Another class of random fields that has attracted considerable attention is that of Markov random fields, defined in some domain 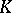 of
of 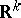 . The condition for a random field
. The condition for a random field 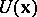 of being Markov asserts, roughly speaking, that for a sufficiently large family of open sets
of being Markov asserts, roughly speaking, that for a sufficiently large family of open sets 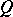 with boundary
with boundary 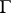 , fixing the values taken by the field in the
, fixing the values taken by the field in the  -neighbourhood
-neighbourhood 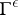 of
of 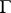 for any
for any  gives that the families of random variables
gives that the families of random variables 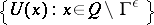 and
and 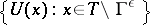 , where
, where 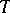 is the complement of the closure of
is the complement of the closure of 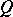 in
in  , are mutually independent (or, in the case of the Markov property in the wide sense, mutually uncorrelated; see, for example, [5]). This can be generalized to the concept of
, are mutually independent (or, in the case of the Markov property in the wide sense, mutually uncorrelated; see, for example, [5]). This can be generalized to the concept of 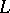 -Markov random fields, where the above independence (or orthogonality) need only hold when the
-Markov random fields, where the above independence (or orthogonality) need only hold when the  -neighbourhood
-neighbourhood  of arbitrary width is replaced by a special type of thickened boundary
of arbitrary width is replaced by a special type of thickened boundary  . The theory of Markov random fields and
. The theory of Markov random fields and 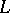 -Markov fields has a number of important applications in quantum field theory and statistical physics (see [6], [7]). Another class of random fields arising from problems of statistical physics is that of Gibbs random fields, whose probability distributions can be expressed as Gibbs distributions (cf. Gibbs distribution; see e.g. [7], [8], [10]). A convenient way of defining Gibbs random fields involves a family of conditional probability distributions of values of the field in a finite domain corresponding to all its fixed values outside this domain. It must be noted that it is often convenient to regard random fields on a smooth manifold
-Markov fields has a number of important applications in quantum field theory and statistical physics (see [6], [7]). Another class of random fields arising from problems of statistical physics is that of Gibbs random fields, whose probability distributions can be expressed as Gibbs distributions (cf. Gibbs distribution; see e.g. [7], [8], [10]). A convenient way of defining Gibbs random fields involves a family of conditional probability distributions of values of the field in a finite domain corresponding to all its fixed values outside this domain. It must be noted that it is often convenient to regard random fields on a smooth manifold 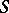 as a special case of generalized random fields, for which there may not exist values at one specified point, but the smoothened values
as a special case of generalized random fields, for which there may not exist values at one specified point, but the smoothened values  can be interpreted as random linear functionals defined on some space
can be interpreted as random linear functionals defined on some space  of smooth test functions
of smooth test functions 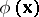 . Generalized random fields (and especially generalized Markov random fields) are widely used in physical applications. By considering within the limits of the theory of generalized random fields (cf. Random field, generalized) the fields
. Generalized random fields (and especially generalized Markov random fields) are widely used in physical applications. By considering within the limits of the theory of generalized random fields (cf. Random field, generalized) the fields 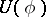 , where the
, where the 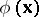 are such that
are such that
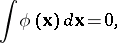 |
it is also possible to define the concepts of the locally homogeneous (and locally homogeneous and locally isotropic) random fields related to stochastic processes with stationary increments (cf. Stochastic process with stationary increments); see [10], . Such fields play an important role in the statistical theory of turbulence (see, for example, [1], [9]).
References
| [1] | A.S. Monin, A.M. Yaglom, "Statistical fluid mechanics" , 1–2 , M.I.T. (1971–1975) (Translated from Russian) |
| [2] | A.P. Khusu, Yu.R. Vitenberg, V.A. Pal'mov, "Surface roughness (a probabilistic approach)" , Moscow (1975) (In Russian) |
| [3] | E.J. Hannan, "Group representations and applied probability" , Methuen (1965) |
| [4] | M.I. Yadrenko, "Spectral theory of random fields" , Optim. Software (1983) (Translated from Russian) |
| [5] | Yu.A. Rozanov, "Markov random fields" , Springer (1982) (Translated from Russian) |
| [6] | B. Simon, "The 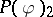 Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [7] | K. Preston, "Gibbs states on countable sets" , Cambridge Univ. Press (1974) |
| [8] | R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , Multi-component random systems , M. Dekker (1980) (Translated from Russian) |
| [9] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1964) (Translated from Russian) |
| [10] | V.A. Malyshev, R.A. Minlos, "Gibbs random fields" , Kluwer (1990) (Translated from Russian) |
Comments
For Gibbs and Markov fields see also [a2]–[a3]. The estimation theory of random fields is discussed in [a4]–[a5]. For limit theorems concerning random fields cf. [a5].
References
| [a1] | J. Adler, "The geometry of random fields" , Wiley (1981) |
| [a2] | S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Non standard methods in stochastic analysis and mathematical physics" , Acad. Press (1986) |
| [a3] | H.-O. Georgii, "Gibbs measures and phase transitions" , de Gruyter (1988) |
| [a4] | A.G. Ramm, "Random fields: estimation theory" , Longman & Wiley (1990) |
| [a5] | A.V. Ivanov, N.N. Leonenko, "Statistical analysis of random fields" , Kluwer (1989) (Translated from Russian) |
Random field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_field&oldid=38532