Difference between revisions of "Symmetric channel"
(Importing text file) |
|||
| Line 1: | Line 1: | ||
| − | A [[Communication channel|communication channel]] whose transition function possesses some kind of symmetry. A homogeneous discrete time [[Memoryless channel|memoryless channel]] with finite alphabets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916001.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916002.png" /> of input and output letters, respectively, and defined by a matrix of transition probabilities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916003.png" /> is called a symmetric channel if | + | A [[Communication channel|communication channel]] whose transition function possesses some kind of symmetry. A homogeneous discrete time [[Memoryless channel|memoryless channel]] with finite alphabets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916001.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916002.png" /> of input and output letters, respectively, and defined by a matrix of transition probabilities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916003.png" /> is called a symmetric channel if: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916004.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s091/s091600/s0916004.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | ||
Revision as of 00:44, 14 April 2015
A communication channel whose transition function possesses some kind of symmetry. A homogeneous discrete time memoryless channel with finite alphabets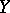 
and 
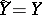of input and output letters, respectively, and defined by a matrix of transition probabilities 
is called a symmetric channel if:
 | (*) |
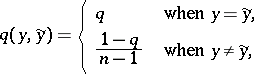where 
is the number of elements of 
, 
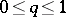. The most studied example of a memoryless symmetric channel is the binary symmetric channel with matrix of transition probabilities
 |
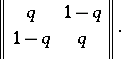For symmetric channels, many important information-theoretic characteristics can either be calculated explicitly or their calculation can be substantially simplified in comparison with non-symmetric channels. For example, for a memoryless symmetric channel with matrix 
of the form (*) the capacity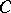 
(cf. Transmission rate of a channel) is given by the equation
 |
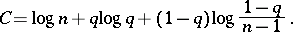For references see ,
cited under Communication channel.
Comments
References
| [a1] | R.C. Gallager, "Information theory and reliable communication" , Wiley (1968) |
Symmetric channel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_channel&oldid=36402