Difference between revisions of "User talk:WikiSysop"
m |
|||
| Line 6: | Line 6: | ||
Test | Test | ||
==Test Asymptote== | ==Test Asymptote== | ||
| + | ===Tests November 1th=== | ||
| + | ====Case 1==== | ||
| + | <asy> | ||
| + | size(0,100); | ||
| + | pair z1=(-1,0); | ||
| + | pair z2=(1,0); | ||
| + | real r=1.5; | ||
| + | path c1=circle(z1,r); | ||
| + | path c2=circle(z2,r); | ||
| + | fill(c1, lightred); | ||
| + | fill(c2, lightgreen); | ||
| + | picture intersection; | ||
| + | fill(intersection,c1,lightred+lightgreen); | ||
| + | clip(intersection,c2); | ||
| + | add(intersection); | ||
| + | draw(c1); | ||
| + | draw(c2); | ||
| + | label("$A$",z1); | ||
| + | label("$B$",z2); | ||
| + | path g=(0,-2)--(0,-0.25); | ||
| + | draw(Label("$A\cap B$",0),g,Arrow); | ||
| + | </asy> | ||
===Tests November 17th=== | ===Tests November 17th=== | ||
====Case 1==== | ====Case 1==== | ||
Revision as of 16:52, 25 November 2014
Test Copy&Paste HTML
Test Test
Test Asymptote
Tests November 1th
Case 1
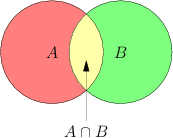
Tests November 17th
Case 1
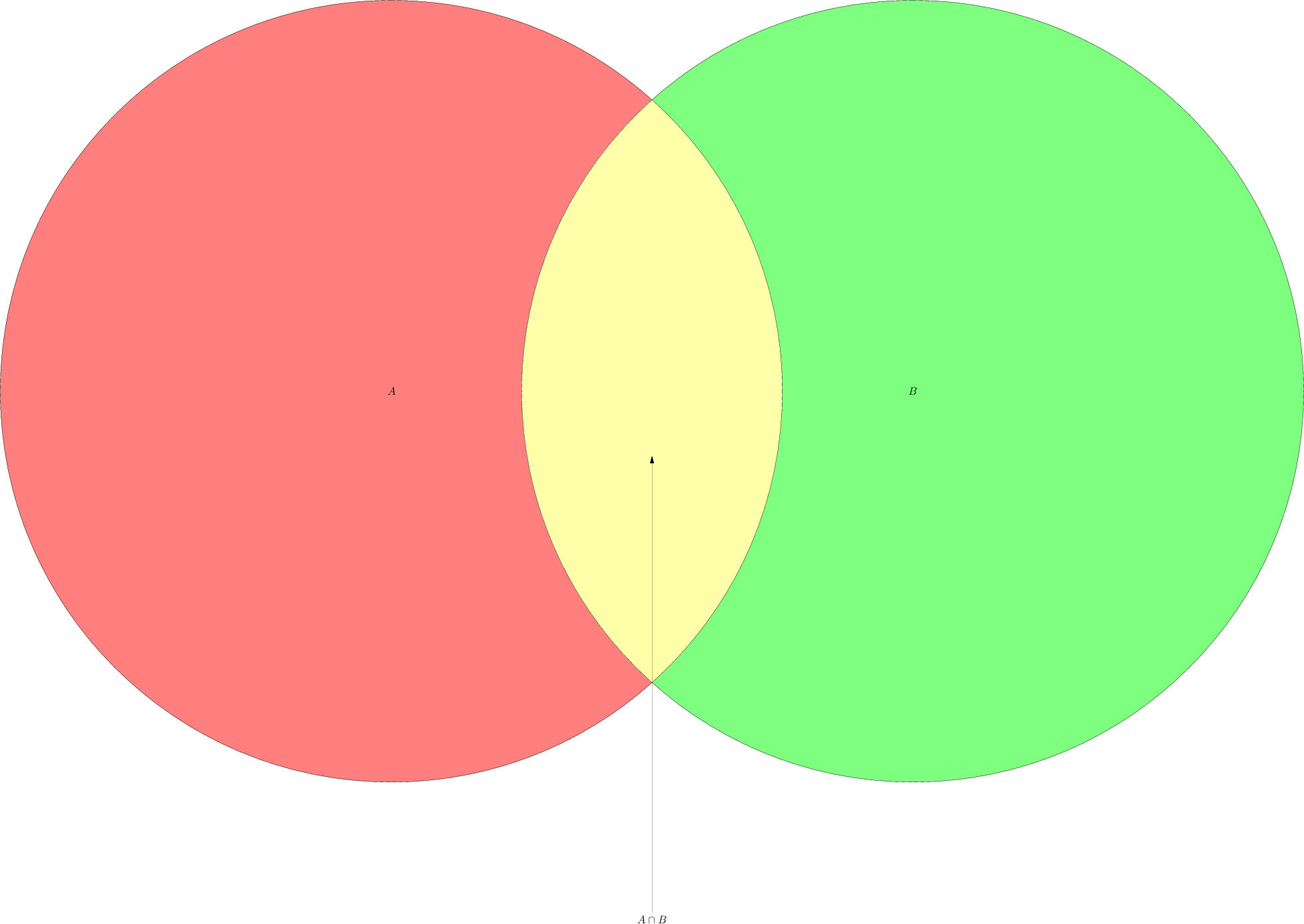
Tests November 4th
Case 1

Case 2
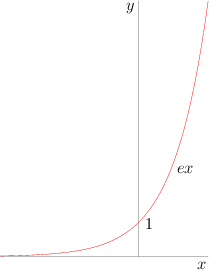
Case 3
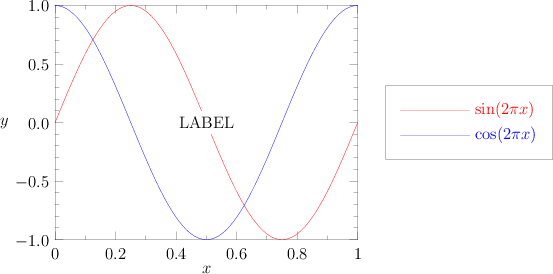
Tests October 27th
Case 1


Case 2
Case 3
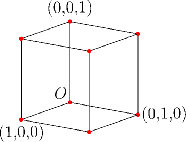
Case 4

Case 5
[asy] pair A,B,C,X,Y,Z; A = (0,0); B = (1,0); C = (0.3,0.8); draw(A--B--C--A); X = (B+C)/2; Y = (A+C)/2; Z = (A+B)/2; draw(A--X, red); draw(B--Y,red); draw(C--Z,red); [/asy]
Previous tests










Test Cite Extension
Example: Cite-Extension
Test MathJax
\begin{align} \dot{x} & = \sigma(y-x) \\ \dot{y} & = \rho x - y - xz \\ \dot{z} & = -\beta z + xy \end{align}
\[
\frac{1}{(\sqrt{\phi \sqrt{5}}-\phi) e^{\frac25 \pi}} =
1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}}
{1+\frac{e^{-8\pi}} {1+\ldots} } } }
\]
Some Text \( \frac{1}{(\sqrt{\phi \sqrt{5}}-\phi) e^{\frac25 \pi}} = 1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}} {1+\frac{e^{-8\pi}} {1+\ldots} } } } \)
Some Text
\[
\frac{1}{(\sqrt{\phi \sqrt{5}}-\phi) e^{\frac25 \pi}} =
1+\frac{e^{-2\pi}} {1+\frac{e^{-4\pi}} {1+\frac{e^{-6\pi}}
{1+\frac{e^{-8\pi}} {1+\ldots} } } }
\]
Pages A-Z
Alphabetically ordered index of all pages
Recent Changes
List of previous changes on EOM
.
WikiSysop. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=WikiSysop&oldid=34969
Test January 12th 2015