Namespaces
Variants
Actions

Difference between revisions of "User:Boris Tsirelson/sandbox2"

From Encyclopedia of Mathematics
Jump to: navigation, search
("Asymptote" does not work yet)
Line 1: Line 1:
 +
<center><asy>
 +
int M=30;
 +
real a = 0.07;
 +
real a0 = 0.15;
 +
real b = 0.02;
 +
real c = 0.6;
 +
real d = -0.2;
 +
real x0 = -0.22;
 +
real u = 0.2;
 +
real v = 0.32;
 +
 +
draw ((-0.7,0)--(0.3,0),Arrow);
 +
draw ((x0,-0.02)--(x0,1.2),Arrow);
 +
 +
label("$x$",(0.3,0),E);
 +
label(rotate(90)*"$y$",(x0,1.2),N);
 +
label("$x_0$",(x0,-0.02),S);
 +
 +
guide g1; guide g2; guide g3; guide g4; guide g5;
 +
for (int k=floor(-0.7M); k<floor(0.3M); ++k) {
 +
  real x = k/M;
 +
  real z = 1+3*x^2;
 +
  real y1 = 1/(z-2a-a0)+2b*(1+c*x)+d;
 +
  real y2 = 1/(z-a-a0)+b*(1+c*x)+d;
 +
  real y3 = 1/(z-a0)+d;
 +
  real y4 = 1/(z+a-a0)-b*(1+c*x)+d;
 +
  real y5 = 1/(z+2a-a0)-2b*(1+c*x)+d;
 +
  g1=g1..(x,y1);
 +
  g2=g2..(x,y2);
 +
  g3=g3..(x,y3);
 +
  g4=g4..(x,y4);
 +
  g5=g5..(x,y5);
 +
}
 +
draw(g1,defaultpen+1);
 +
draw(g2,defaultpen+1);
 +
draw(g3,defaultpen+1);
 +
draw(g4,defaultpen+1);
 +
draw(g5,defaultpen+1);
 +
 +
real x = x0;
 +
real z = 1+3*x^2;
 +
real y1 = 1/(z-2a-a0)+2b*(1+c*x)+d;
 +
real y2 = 1/(z-a-a0)+b*(1+c*x)+d;
 +
real y3 = 1/(z-a0)+d;
 +
real y4 = 1/(z+a-a0)-b*(1+c*x)+d;
 +
real y5 = 1/(z+2a-a0)-2b*(1+c*x)+d;
 +
path g = (x,y1)..(x-u,y2)..(x-v,y3)..(x-u,y4)..(x,y5);
 +
draw( g );
 +
 +
pair w = (0.1,-0.6);
 +
 +
pair p = point(g,0.5);
 +
dot ( p );
 +
draw( p--p-0.5w, dashed );
 +
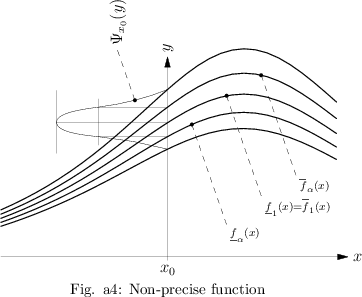
label(rotate(90)*"$\Psi_{x_0}(y)$",p-0.5w,N);
 +
 +
draw( (x,y2)--(x-u,y2) );
 +
draw( (x,y3)--(x-v,y3) );
 +
draw( (x,y4)--(x-u,y4) );
 +
 +
draw( (x-u,y2+0.05)--(x-u,y4-0.05) );
 +
draw( (x-v,y2+0.1)--(x-v,y4-0.1) );
 +
 +
real x = -0.15;
 +
real z = 1+3*x^2;
 +
real y4 = 1/(z+a-a0)-b*(1+c*x)+d;
 +
dot( (x,y4) );
 +
draw( (x,y4)--(x,y4)+w, dashed );
 +
label("$\scriptstyle \underline f_\alpha(x)$",(x,y4)+w,SE);
 +
 +
real x = -0.05;
 +
real z = 1+3*x^2;
 +
real y3 = 1/(z-a0)+d;
 +
dot( (x,y3) );
 +
draw( (x,y3)--(x,y3)+w, dashed );
 +
label("$\scriptstyle \underline f_1(x)=\overline f_1(x)$",(x,y3)+w,SE);
 +
 +
real x = 0.05;
 +
real z = 1+3*x^2;
 +
real y2 = 1/(z-a-a0)+b*(1+c*x)+d;
 +
dot( (x,y2) );
 +
draw( (x,y2)--(x,y2)+w, dashed );
 +
label("$\scriptstyle \overline f_\alpha(x)$",(x,y2)+w,SE);
 +
 +
label("\small Fig. a4: Non-precise function",(x0,-0.2));
 +
 +
shipout(scale(250,120)*currentpicture);
 +
</asy></center>
 +
 
<center><asy>
 
<center><asy>
 
import gsl;
 
import gsl;

Revision as of 21:54, 12 November 2014






[Calculus: ] the art of numbering and measuring exactly a thing whose existence cannot be conceived. (Voltaire, Letter XVII: On Infinites In Geometry, And Sir Isaac Newton's Chronology)

And what are these fluxions? The velocities of evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities? (Berkeley, The Analyst)


WARNING: Asirra, the cat and dog CAPTCHA, is closing permanently on October 6, 2014. Please contact this site's administrator and ask them to switch to a different CAPTCHA. Thank you!

How to Cite This Entry:
Boris Tsirelson/sandbox2. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boris_Tsirelson/sandbox2&oldid=34474
Retrieved from "https://encyclopediaofmath.org/index.php?title=User:Boris_Tsirelson/sandbox2&oldid=34474"