Difference between revisions of "User:Boris Tsirelson/sandbox2"
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | the method is as follows: | ||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560602.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560603.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560604.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560605.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560606.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560607.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k056/k056060/k0560608.png" /></td> </tr></table> | ||
| + | |||
| + | The number | ||
******************************************* | ******************************************* | ||
Revision as of 20:00, 22 July 2014
the method is as follows:
 | (2) |
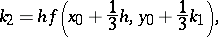 |
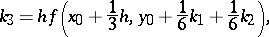 |
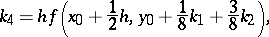 |
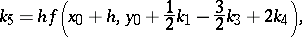 |
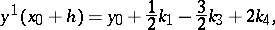 |
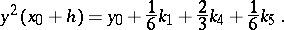 |
The number
$$\text{ $K$ compact}$$
\[\text{ '"`UNIQ-MathJax2-QINU`"' compact}\]
\begin{equation} \mu (B)= \sup \{\mu(K): K\subset B, \text{ '"`UNIQ-MathJax3-QINU`"' compact}\}\, \end{equation}
and having the following property: \begin{equation}\label{e:tight} \mu (B)= \sup \{\mu(K): K\subset B, \mbox{ '"`UNIQ-MathJax4-QINU`"' compact}\}\, \end{equation} (see [Sc]).
The total variation measure of a $\mathbb C$-valued measure is defined on $\mathcal{B}$ as:
\[
\abs{\mu}(B) :=\sup\left\{ \sum \abs{\mu(B_i)}: \text{$\{B_i\}\subset\mathcal{B}'"`UNIQ-MathJax7-QINU`"'B$}\right\}.
\]
In the real-valued case the above definition simplifies as
and the following identity holds: \begin{equation}\label{e:area_formula} \int_A J f (y) \, dy = \int_{\mathbb R^m} \mathcal{H}^0 (A\cap f^{-1} (\{z\}))\, d\mathcal{H}^n (z)\, . \end{equation}
Cp. with 3.2.2 of [EG]. From \eqref{e:area_formula} it is not difficult to conclude the following generalization (which also goes often under the same name):
\begin{equation}\label{ab}
E=mc^2
\end{equation}
By \eqref{ab}, it is possible. But see \eqref{ba} below:
\begin{equation}\label{ba}
E\ne mc^3,
\end{equation}
which is a pity.
Boris Tsirelson/sandbox2. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boris_Tsirelson/sandbox2&oldid=32515