Schwarz integral

A parameter-dependent integral that gives a solution to the Schwarz problem on expressing an analytic function 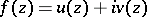in the unit disc by the boundary values of its real (or imaginary) part on the boundary circle (see [1]).

Let on the unit circle 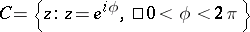a continuous real-valued function 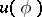be given. Then the Schwarz integral formulas defining an analytic function 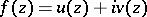, the boundary values of whose real part coincide with 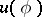(or the boundary values of whose imaginary part coincide with 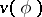), have the form

(*)

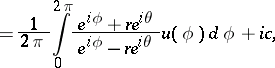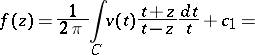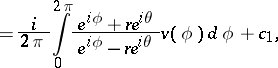where , , 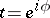and and are arbitrary real constants. The Schwarz integral (*) is closely connected with the Poisson integral. The expression

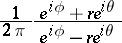is often called the Schwarz kernel, and the integral operator in the first formula of (*) is called the Schwarz operator. These notions can be generalized to the case of arbitrary domains in the complex plane (see [3]). The Schwarz integral and its generalizations are very important when solving boundary value problems of analytic function theory (see also [3]) and when studying boundary properties of analytic functions (see also [4]).

When applying the integral formulas (*), a very important and more difficult problem arises concerning the existence and the expression of the boundary values of the imaginary part 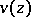and of the complete function 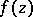by the given boundary values of the real part 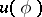(or of expressing the boundary values of the real part 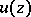and those of the complete function 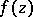by the given boundary values of the imaginary part 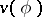). If the given functions 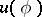or 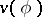satisfy a Hölder condition on 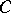, then the corresponding boundary values of or are expressed by the Hilbert formulas

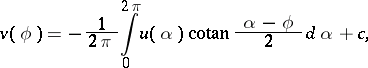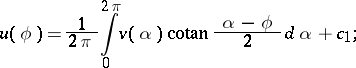here the integrals in these formulas are singular integrals and exist in the Cauchy principal-value sense (see [3], and also Hilbert singular integral).

References

[1]	H.A. Schwarz, "Gesamm. math. Abhandl." , 2 , Springer (1890)
[2]	A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian)
[3]	F.D. Gakhov, "Boundary value problems" , Pergamon (1966) (Translated from Russian)
[4]	I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)

Comments

The Schwarz problem is closely related to the Dirichlet problem: Given the real part 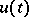of the boundary value of 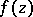, the harmonic function 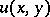is found from it and then the conjugate harmonic function 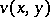is determined from via the Cauchy-Riemann equations; cf. [3], Sect. 27.2.