Liouville-Łojasiewicz inequality

A Liouville inequality is one embodying the principle in number theory that algebraic numbers cannot be very well approximated by rational numbers or, equivalently, that integral polynomials cannot be small and non-zero at algebraic numbers (cf. also Liouville theorems). A Łojasiewicz inequality gives a lower bound for functions in terms of the distance to common zeros, see also Lojasiewciz inequality.

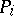These features can be combined [a5] in the following Liouville–Łojasiewicz inequality. Let each have total degree at most and coefficients of absolute value at most . For , let be greater than or equal to the largest absolute value of the coordinates of and let be less than or equal to the distance from to the common zeros of . Then there are explicit constants 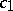, , 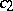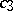depending on such that

where , .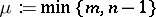

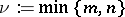Over arbitrary fields with an absolute value, the lower bound takes the form 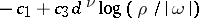, cf. [a4], [a2] and [a1] (in the last citation, the polynomials 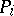are replaced by ideals and 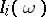are taken to be the values of fixed Chow coordinates of 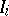). In this setting, M. Hickel [a3] obtains the optimal involvement of 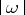at the right-hand side. Actually, the above arithmetic inequality holds with .

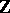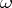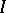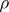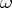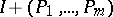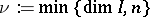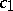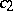If, when working over , denotes a zero of an unmixed ideal and denotes the distance from to the zeros of , then the above upper bound holds with , , with replaced by , and by 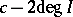. When 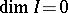, the zeros 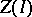of 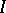have algebraic coordinates. When 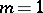and 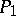does not vanish at any point of , then one obtains an explicit lower bound on 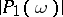, i.e. a Liouville inequality.

References

[a1]	J. Kollár, "Effective Nullstellensatz for arbitrary ideals" J. Europ. Math. Soc. (JEMS) , 1 (1999) pp. 313–337
[a2]	S. Ji, J. Kollár, B. Shiffman, "A global Łojasiewicz inequality for algebraic varieties" Trans. Amer. Math. Soc. , 329 (1992) pp. 813–818
[a3]	M. Hickel, "Solution d'une conjecture de C. Berenstein–A. Yger et invariants de contact à l'infini" Prepubl. Lab. Math. Pures Univ. Bordeaux I , 118 : jan. (2000)
[a4]	W.D. Brownawell, "Bounds for the degrees in the Nullstellensatz" Ann. of Math. , 126 (1987) pp. 577–591
[a5]	W.D. Brownawell, "Local diophantine Nullstellen equalities" J. Amer. Math. Soc. , 1 (1988) pp. 311–322