Difference between revisions of "Z-transform"
(Importing text file) |
m (→Example.: TeXed the first equation which was urgently needed, as there was a missing parenthesis before "20 x ( n + 1 + 24 x ..." after "20 x ( n + 1 ) + 24 x ...") |
||
| Line 72: | Line 72: | ||
The most practical method of finding the inverse Z-transform is the use of partial-fractions techniques as illustrated by the following example. | The most practical method of finding the inverse Z-transform is the use of partial-fractions techniques as illustrated by the following example. | ||
| + | |||
| + | |||
===Example.=== | ===Example.=== | ||
| − | See also [[#References|[a2]]]. Suppose the problem is to solve the difference equation | + | See also [[#References|[a2]]]. Suppose the problem is to solve the difference equation |
| + | |||
| + | \begin{equation} | ||
| + | x \left( n + 4 \right) + 9 x \left( n + 3 \right) + 30 x \left( n + 2 \right) + 20 x \left( n + 1 \right) + 24 x \left( n \right) = 0 , | ||
| + | \end{equation} | ||
| + | |||
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/z/z130/z130010/z13001052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/z/z130/z130010/z13001053.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/z/z130/z130010/z13001054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/z/z130/z130010/z13001055.png" />. | ||
Taking the Z-transform yields | Taking the Z-transform yields | ||
Revision as of 09:13, 31 October 2013
Z-transformation
This transform method may be traced back to A. De Moivre [a5] around the year 1730 when he introduced the concept of "generating functions" in probability theory. Closely related to generating functions is the Z-transform, which may be considered as the discrete analogue of the Laplace transform. The Z-transform is widely used in the analysis and design of digital control, and signal processing [a4], [a2], [a3], [a6].
The Z-transform of a sequence 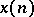 ,
, 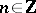 , that is identically zero for negative integers, is defined as
, that is identically zero for negative integers, is defined as
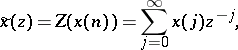 | (a1) |
where  is a complex number.
is a complex number.
By the root test, the series (a1) converges if 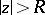 , where
, where 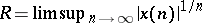 . The number
. The number 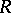 is called the radius of convergence of the series (a1).
is called the radius of convergence of the series (a1).
Example 1.
The Z-transform of 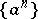 is given by
is given by
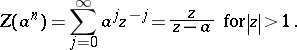 |
Example 2.
The Z-transform of the Kronecker-delta sequence
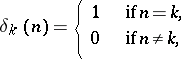 |
is given by
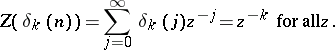 |
Properties of the Z-transform.
i) Linearity: Let  and
and  be the radii of convergence of the sequences
be the radii of convergence of the sequences 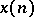 and
and 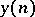 . Then for any
. Then for any 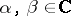 ,
,
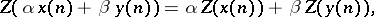 |
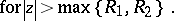 |
ii) Shifting: Let 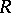 be the radius of convergence of
be the radius of convergence of 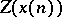 . Then, for
. Then, for 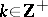 ,
,
a) Right-shifting: 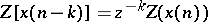 , for
, for 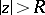 ;
;
b) Left-shifting: 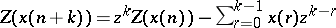 , for
, for 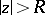 .
.
iii) Initial and final value.
a) Initial value theorem: 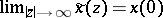 ;
;
b) Final value theorem: 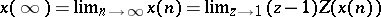 .
.
iv) Convolution: The convolution of two sequences 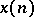 and
and 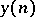 is defined by
is defined by
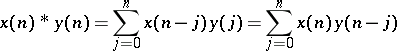 |
and its Z-transform is given by
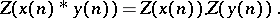 |
Inverse Z-transform.
If 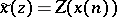 , then the inverse Z-transform is defined as
, then the inverse Z-transform is defined as 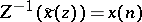 . Notice that by Laurent's theorem [a1] (cf. also Laurent series), the inverse Z-transform is unique [a2]. Consider a circle
. Notice that by Laurent's theorem [a1] (cf. also Laurent series), the inverse Z-transform is unique [a2]. Consider a circle  centred at the origin of the
centred at the origin of the  -plane and enclosing all the poles of
-plane and enclosing all the poles of 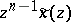 . Then, by the Cauchy integral theorem [a1], the inversion formula is given by
. Then, by the Cauchy integral theorem [a1], the inversion formula is given by
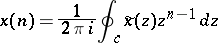 |
and by the residue theorem (cf. also Residue of an analytic function) [a1], 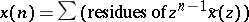 .
.
If 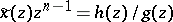 in its reduced form, then the poles of
in its reduced form, then the poles of 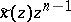 are the zeros of
are the zeros of 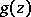 .
.
a) If 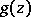 has simple zeros, then the residue
has simple zeros, then the residue 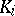 corresponding to the zero
corresponding to the zero 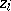 is given by
is given by
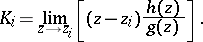 |
b) If 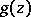 has multiple zeros, then the residue
has multiple zeros, then the residue 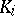 at the zero
at the zero 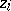 with multiplicity
with multiplicity  is given by
is given by
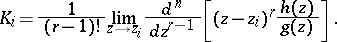 |
The most practical method of finding the inverse Z-transform is the use of partial-fractions techniques as illustrated by the following example.
Example.
See also [a2]. Suppose the problem is to solve the difference equation
\begin{equation} x \left( n + 4 \right) + 9 x \left( n + 3 \right) + 30 x \left( n + 2 \right) + 20 x \left( n + 1 \right) + 24 x \left( n \right) = 0 , \end{equation}
where 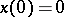 ,
, 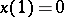 ,
, 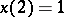 ,
, 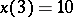 .
.
Taking the Z-transform yields
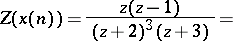 |
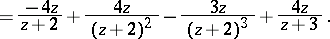 |
Taking the inverse Z-transform of both sides yields
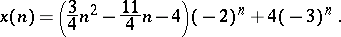 |
Pairs of Z-transforms.
'
<tbody> </tbody>
|
References
| [a1] | R.V. Churchill, J.W. Brown, "Complex variables and applications" , McGraw-Hill (1990) |
| [a2] | S. Elaydi, "An introduction to difference equations" , Springer (1999) (Edition: Second) |
| [a3] | A.J. Jerri, "Linear difference equations with discrete transform methods" , Kluwer Acad. Publ. (1996) |
| [a4] | E. Jury, "Theory and application of the z-transform method" , Robert E. Krieger (1964) |
| [a5] | A. De Moivre, "Miscellanew, Analytica de Seriebus et Quatratoris" , London (1730) |
| [a6] | A.D. Poularikas, "The transforms and applications" , CRC (1996) |
Z-transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Z-transform&oldid=30630
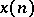
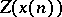
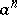
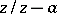
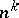

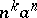
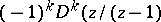 ;
; 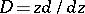

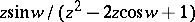
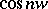
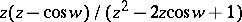
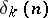
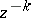
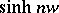
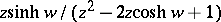

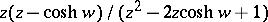 .
.