Difference between revisions of "Proposition"
m (remove the double vision, and map a link) |
m (swap the argument with its value) |
||
| Line 15: | Line 15: | ||
====Comments==== | ====Comments==== | ||
| − | In Western parlance, the term "proposition" tends to be reserved for formulas in a language not involving variables at all (cf. [[Propositional calculus|Propositional calculus]]). The term [["sentence" | + | In Western parlance, the term "proposition" tends to be reserved for formulas in a language not involving variables at all (cf. [[Propositional calculus|Propositional calculus]]). The term [[sentence|"sentence"]] is used for a formula whose variables are all quantified, as in the examples above. |
Revision as of 15:28, 19 June 2013
The simplest expression of a language. It is a concatenation of words that has an independent meaning, i.e. expresses a complete statement. In formalized languages a proposition is a formula without free variables, i.e. parameters. In formalized languages a proposition is also called a closed formula. E.g., in a first-order language (the language of the narrow predicate calculus) the formulas
 |
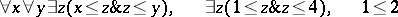are closed (the first is false, the second and third are true in the domain of natural numbers). The formulas
 |
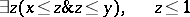are not closed, i.e. contain parameters (
and 
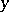in the first, 
in the second).
References
| [1] | A. Church, "Introduction to mathematical logic" , 1 , Princeton Univ. Press (1956) |
Comments
In Western parlance, the term "proposition" tends to be reserved for formulas in a language not involving variables at all (cf. Propositional calculus). The term "sentence" is used for a formula whose variables are all quantified, as in the examples above.
Proposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Proposition&oldid=29861