Difference between revisions of "Vinogradov method"
(Importing text file) |
(Started TeX) |
||
| Line 3: | Line 3: | ||
One distinguishes two parts in Vinogradov's method: The method of estimating Weyl sums (cf. [[Weyl sum|Weyl sum]]) and the method of estimating trigonometric sums with prime numbers. Both these parts utilize Vinogradov's basic idea — to wit, the idea of smoothing double trigonometric sums, which may be described as follows. Given the sum | One distinguishes two parts in Vinogradov's method: The method of estimating Weyl sums (cf. [[Weyl sum|Weyl sum]]) and the method of estimating trigonometric sums with prime numbers. Both these parts utilize Vinogradov's basic idea — to wit, the idea of smoothing double trigonometric sums, which may be described as follows. Given the sum | ||
| − | + | \[ W=\sum_u\sum_v\psi_1(u)\psi_2(v) e^{2\pi i\alpha uv},\] | |
| − | where the summation variables | + | where the summation variables $u$ and $v$ run through the values of (not necessarily successive) integers in respective sets $U$ and $V$, $A<u<2A$. Let $\psi_1(u)$ and $\psi_2(v)$ be arbitrary complex-valued functions. Then |
| − | < | + | \[ \lvert W\rvert^2\leq B\sum_{A< u\leq 2A}\left\lvert \sum_v\psi_2(v)e^{2\pi i\alpha uv}\right\rvert^2,\] |
| − | where | + | where $u$ runs through the successive integers in the interval $(A,2A]$ (smoothing), and |
| − | + | \[ B=\sum_n\lvert \psi_1(u)\rvert^2.\] | |
==Vinogradov's method for estimating Weyl sums.== | ==Vinogradov's method for estimating Weyl sums.== | ||
The sums to be estimated are | The sums to be estimated are | ||
| − | + | \[ S=\sum_{1\leq x\leq P}e^{2\pi if(x)},\] | |
| − | where | + | where $f(x)=\alpha_{n+1}x^{n+1}+\cdots+\alpha_1x$; here $\alpha_{n+1},\ldots,\alpha_1$ are real numbers. For $Y=[P^{1-n^2/4}]$ one finds |
| − | + | \begin{align*} | |
| + | S&=Y^{-1}\sum_{1\leq x\leq P}\sum_{1\leq y\leq Y}e^{2\pi if(x+y)}+2\theta Y\\ | ||
| + | &=Y^{-1}\sum_{1\leq x\leq P}\sum_{1\leq y\leq Y}e^{2\pi i\mathfrak{A}}+2\theta Y=Y^{-1}W+2\theta Y,\] | ||
| − | + | where $\mathfrak{A}=\alpha_{n+1}x^{n+1}+A_n(y)x^n+\cdots+A_1(y)x+A_0(y)$, the letter $W$ denotes the double sum over $x$ and $y$, and $\lvert \theta\rvert\leq 1$. Moreover, letting $\mathfrak{B}$ denote the expression | |
| − | + | \[ \alpha_{n+1}x^{n+1}+(A_n(y)+B_n)x^n+\cdots+(A_1(y)+B_1)x\] | |
| − | |||
| − | |||
one has | one has | ||
| − | + | \[\lvert W\rvert\leq \sum_{1\leq y\leq Y}\left\lvert \sum_{1\leq x\leq P}e^{2\pi i\mathfrak{B}}\right\rvert+Y_nP^{1-n^2/4},\] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | for arbitrary $B_n,\ldots,B_1$ from the domain | |
| − | + | \[\lvert B_n\rvert\leq L_n=P^{-n-n^2/4},\textrm{\,\,\,\,\,}\ldots\textrm{\,\,\,\,}\lvert B_1\rvert\leq L_1=P^{-1-n^2/4}.\] | |
| − | + | For any integer $k\geq 1$: | |
| − | + | \[ \lvert W\rvert^{2k}\leq 2^kY^{2k-1}\sum_{1\leq y\leq Y}\int_{\lvert B_n\rvert\leq L_n}\cdots \int_{\lvert B_1\rvert\leq L_1} | |
| + | \left\lvert \sum_{1\leq x\leq P} e^{2\pi i\mathfrak{B}}\right\rvert\mathrm{d}B_n\cdots\mathrm{d}B_1 | ||
| + | +2^k(Y_nP^{1-n^2/4})^{2k}\] | ||
| + | \[\leq 2^kY^{2k-1}G(Y)\int_0^1\cdots \int_0^1\left\lvert \sum_{1\leq x\leq P}e^{2\pi i\mathfrak{C}}\right\rvert^{2k} | ||
| + | \mathrm{d}\gamma_n\cdots\mathrm{d}\gamma_1+2^k(Y_nP^{1-n^2/4})^{2k},\] | ||
| − | + | where $\mathfrak{C}=\alpha_{n+1}x^{n+1}+\gamma_nx^n+\cdots+\gamma_1x$ and $G(Y)$ is the maximum number of cases of coincidence of points with coordinates | |
| − | + | \[ \{A_n(y)+B_n\},\{A_{n-1}(y)+B_{n-1}\},\ldots,\{A_1(y)+B_1\}.\] | |
| − | |||
| − | Here the braces denote the fractional part of the enclosed number, while | + | Here the braces denote the fractional part of the enclosed number, while $y$ varies between 1 and $Y$, and |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096690/v09669041.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096690/v09669041.png" /></td> </tr></table> | ||
Revision as of 08:17, 17 June 2013
A new method for estimating trigonometric sums (see Trigonometric sums, method of). By Vinogradov's method one may obtain very accurate estimates of a wide class of trigonometric sums, in which the summation variable runs through a sequence of integers, prime numbers, etc. In this way many classical problems in analytic number theory can be solved (the distribution of the fractional parts of a wide class of functions, the distribution of prime numbers in series of natural numbers, additive problems such as the Waring and Goldbach problems, etc.).
One distinguishes two parts in Vinogradov's method: The method of estimating Weyl sums (cf. Weyl sum) and the method of estimating trigonometric sums with prime numbers. Both these parts utilize Vinogradov's basic idea — to wit, the idea of smoothing double trigonometric sums, which may be described as follows. Given the sum
\[ W=\sum_u\sum_v\psi_1(u)\psi_2(v) e^{2\pi i\alpha uv},\]
where the summation variables $u$ and $v$ run through the values of (not necessarily successive) integers in respective sets $U$ and $V$, $A<u<2A$. Let $\psi_1(u)$ and $\psi_2(v)$ be arbitrary complex-valued functions. Then
\[ \lvert W\rvert^2\leq B\sum_{A< u\leq 2A}\left\lvert \sum_v\psi_2(v)e^{2\pi i\alpha uv}\right\rvert^2,\]
where $u$ runs through the successive integers in the interval $(A,2A]$ (smoothing), and
\[ B=\sum_n\lvert \psi_1(u)\rvert^2.\]
Vinogradov's method for estimating Weyl sums.
The sums to be estimated are
\[ S=\sum_{1\leq x\leq P}e^{2\pi if(x)},\]
where $f(x)=\alpha_{n+1}x^{n+1}+\cdots+\alpha_1x$; here $\alpha_{n+1},\ldots,\alpha_1$ are real numbers. For $Y=[P^{1-n^2/4}]$ one finds
\begin{align*} S&=Y^{-1}\sum_{1\leq x\leq P}\sum_{1\leq y\leq Y}e^{2\pi if(x+y)}+2\theta Y\\ &=Y^{-1}\sum_{1\leq x\leq P}\sum_{1\leq y\leq Y}e^{2\pi i\mathfrak{A}}+2\theta Y=Y^{-1}W+2\theta Y,\]
where $\mathfrak{A}=\alpha_{n+1}x^{n+1}+A_n(y)x^n+\cdots+A_1(y)x+A_0(y)$, the letter $W$ denotes the double sum over $x$ and $y$, and $\lvert \theta\rvert\leq 1$. Moreover, letting $\mathfrak{B}$ denote the expression
\[ \alpha_{n+1}x^{n+1}+(A_n(y)+B_n)x^n+\cdots+(A_1(y)+B_1)x\]
one has
\[\lvert W\rvert\leq \sum_{1\leq y\leq Y}\left\lvert \sum_{1\leq x\leq P}e^{2\pi i\mathfrak{B}}\right\rvert+Y_nP^{1-n^2/4},\]
for arbitrary $B_n,\ldots,B_1$ from the domain
\[\lvert B_n\rvert\leq L_n=P^{-n-n^2/4},\textrm{\,\,\,\,\,}\ldots\textrm{\,\,\,\,}\lvert B_1\rvert\leq L_1=P^{-1-n^2/4}.\]
For any integer $k\geq 1$:
\[ \lvert W\rvert^{2k}\leq 2^kY^{2k-1}\sum_{1\leq y\leq Y}\int_{\lvert B_n\rvert\leq L_n}\cdots \int_{\lvert B_1\rvert\leq L_1} \left\lvert \sum_{1\leq x\leq P} e^{2\pi i\mathfrak{B}}\right\rvert\mathrm{d}B_n\cdots\mathrm{d}B_1 +2^k(Y_nP^{1-n^2/4})^{2k}\] \[\leq 2^kY^{2k-1}G(Y)\int_0^1\cdots \int_0^1\left\lvert \sum_{1\leq x\leq P}e^{2\pi i\mathfrak{C}}\right\rvert^{2k} \mathrm{d}\gamma_n\cdots\mathrm{d}\gamma_1+2^k(Y_nP^{1-n^2/4})^{2k},\]
where $\mathfrak{C}=\alpha_{n+1}x^{n+1}+\gamma_nx^n+\cdots+\gamma_1x$ and $G(Y)$ is the maximum number of cases of coincidence of points with coordinates
\[ \{A_n(y)+B_n\},\{A_{n-1}(y)+B_{n-1}\},\ldots,\{A_1(y)+B_1\}.\]
Here the braces denote the fractional part of the enclosed number, while $y$ varies between 1 and $Y$, and
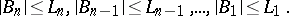 |
If the coefficients 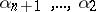 of the polynomial
of the polynomial 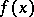 have certain arithmetical properties, it is possible to obtain the estimate
have certain arithmetical properties, it is possible to obtain the estimate 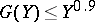 . In addition, the last integral does not exceed the number of solutions of the system of equations:
. In addition, the last integral does not exceed the number of solutions of the system of equations:
 |
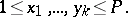 |
The number of solutions of this system is estimated using the Vinogradov theorem about the average, which is fundamental in Vinogradov's method for estimating Weyl sums (cf. Vinogradov estimates).
Vinogradov's method for estimating trigonometric sums with prime numbers.
The sums to be estimated are
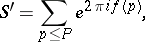 |
where  , and
, and  are real numbers. Let
are real numbers. Let 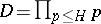 , where
, where 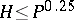 . Using the well-known property of the Möbius function,
. Using the well-known property of the Möbius function, 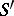 is reduced to a small number of sums (this number is not larger than
is reduced to a small number of sums (this number is not larger than  ) of the form
) of the form
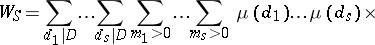 |
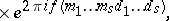 |
where 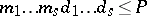 . In the multiple sum
. In the multiple sum 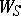 the variables
the variables  run through the entire summation intervals. The sums
run through the entire summation intervals. The sums 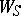 in which the summation interval over at least one variable
in which the summation interval over at least one variable 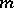 is long are estimated by Vinogradov's method for estimating Weyl sums. Otherwise the summation interval over one of the summation variables
is long are estimated by Vinogradov's method for estimating Weyl sums. Otherwise the summation interval over one of the summation variables 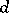 ,
, 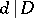 , will be long. In such a case one uses the following lemma of Vinogradov which, together with the idea of smoothing double sums, is fundamental to Vinogradov's method for estimating trigonometric sums with prime numbers.
, will be long. In such a case one uses the following lemma of Vinogradov which, together with the idea of smoothing double sums, is fundamental to Vinogradov's method for estimating trigonometric sums with prime numbers.
Lemma. Let 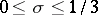 and let
and let 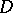 be the product of all primes not larger than
be the product of all primes not larger than 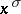 ; all divisors
; all divisors 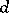 of
of 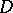 not larger than
not larger than  may then be distributed over fewer than
may then be distributed over fewer than 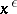 sets with the following properties:
sets with the following properties:
1) the numbers 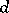 belonging to one of these sets have the same number
belonging to one of these sets have the same number 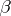 of prime factors and therefore the same value of
of prime factors and therefore the same value of 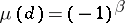 ;
;
2) one of these sets — the so-called simplest set — consists of the single number 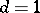 . For each of the remaining sets there is a number
. For each of the remaining sets there is a number 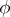 such that all numbers of this set satisfy the relation
such that all numbers of this set satisfy the relation
 |
3) for each set of numbers 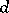 other than the simplest set there exist, for any
other than the simplest set there exist, for any 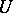 ,
, 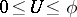 , two sets of numbers
, two sets of numbers 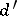 and
and 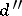 , with corresponding numbers
, with corresponding numbers 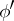 and
and 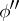 satisfying the relations
satisfying the relations
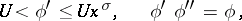 |
and such that, for a certain natural number 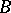 , one obtains each number in the chosen set
, one obtains each number in the chosen set 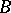 times if, out of all the products
times if, out of all the products 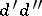 one selects only those which satisfy the relation
one selects only those which satisfy the relation  .
.
The application of point 3) of this lemma, with a suitable value of 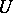 , yields
, yields
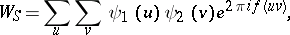 |
where the variables  and
and  run through long summation intervals. It is possible to deduce Vinogradov's estimate for trigonometric sums with prime numbers from this lemma (cf. Vinogradov estimates).
run through long summation intervals. It is possible to deduce Vinogradov's estimate for trigonometric sums with prime numbers from this lemma (cf. Vinogradov estimates).
If 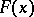 can be properly approximated, in a certain sense, by a polynomial, Vinogradov's method can be used to estimate sums of the type
can be properly approximated, in a certain sense, by a polynomial, Vinogradov's method can be used to estimate sums of the type
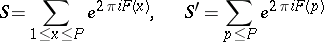 |
(see [2], ). Sums of the type
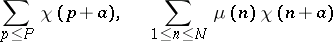 |
and other types can also be estimated by the method. It is possible in this way to solve problems on the distribution of power residues, primitive roots, etc., in sequences of the type 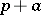 , where
, where 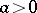 is a given integer, while
is a given integer, while 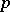 runs through the successive prime numbers [3], [5]. For the application of Vinogradov's method in analytic number theory see [1], [2], , [5], [6].
runs through the successive prime numbers [3], [5]. For the application of Vinogradov's method in analytic number theory see [1], [2], , [5], [6].
References
| [1] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [2] | I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) |
| [3] | I.M. Vinogradov, "Estimates of a sum, distribution of primes in an arithmetic series" Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 481–496 (In Russian) |
| [4a] | A.A. Karatsuba, "Estimates for trigonometric sums by Vinogradov's method, and applications" Proc. Steklov Inst. Math. , 112 (1971) pp. 251–265 Trudy Mat. Inst. Steklov. , 112 (1971) pp. 241–255 |
| [4b] | A.A. Karatsuba, "On some problems of prime number theory connected with I.M. Vinogradov's method" Proc. Steklov Inst. Math. , 132 (1973) pp. 293–298 Trudy Mat. Inst. Steklov. , 132 (1973) pp. 257–261 |
| [5] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
| [6] | K. Chandrasekharan, "Arithmetical functions" , Springer (1970) |
Comments
References
| [a1] | R.C. Vaughan, "The Hardy–Littlewood method" , Cambridge Univ. Press (1981) |
Vinogradov method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vinogradov_method&oldid=29855