Difference between revisions of "Titchmarsh-Weyl m-function"
(Importing text file) |
(TeXified some of the math.) |
||
| Line 1: | Line 1: | ||
A function arising in an attempt to properly determine which singular boundary-value problems are self-adjoint (cf. also [[Self-adjoint differential equation|Self-adjoint differential equation]]). Begin with a formally symmetric differential expression | A function arising in an attempt to properly determine which singular boundary-value problems are self-adjoint (cf. also [[Self-adjoint differential equation|Self-adjoint differential equation]]). Begin with a formally symmetric differential expression | ||
| − | + | $$ | |
| + | L y = \frac{-(p y')' + q y}{w} , | ||
| + | $$ | ||
| − | where | + | where $p\ne 0$, $q,w>0$ are measurable coefficients over $[a,b)$, and which is defined on a domain within $L^2(a,b;w)$. The Titchmarsh–Weyl $m$-function is defined as follows: For $\lambda = \mu + i \nu$, $\nu\ne 0$, let $\phi$ and $\psi$ be solutions of $L y = \lambda y$ satisfying |
| − | + | $$ | |
| + | \begin{aligned} | ||
| + | \phi(a,\lambda) &= \sin\alpha, & \psi(a,\lambda) &= \cos\alpha, \\ | ||
| + | p\phi'(a,\lambda) &= -\cos\alpha, & p\psi'(a,\lambda) &= \sin\alpha . | ||
| + | \end{aligned} | ||
| + | $$ | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120120/t12012014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120120/t12012014.png" /></td> </tr></table> | ||
Revision as of 12:44, 29 October 2012
A function arising in an attempt to properly determine which singular boundary-value problems are self-adjoint (cf. also Self-adjoint differential equation). Begin with a formally symmetric differential expression
$$ L y = \frac{-(p y')' + q y}{w} , $$
where $p\ne 0$, $q,w>0$ are measurable coefficients over $[a,b)$, and which is defined on a domain within $L^2(a,b;w)$. The Titchmarsh–Weyl $m$-function is defined as follows: For $\lambda = \mu + i \nu$, $\nu\ne 0$, let $\phi$ and $\psi$ be solutions of $L y = \lambda y$ satisfying
$$ \begin{aligned} \phi(a,\lambda) &= \sin\alpha, & \psi(a,\lambda) &= \cos\alpha, \\ p\phi'(a,\lambda) &= -\cos\alpha, & p\psi'(a,\lambda) &= \sin\alpha . \end{aligned} $$
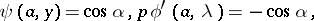 |
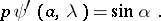 |
Now consider a real boundary condition at  ,
,  , of the form
, of the form
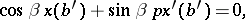 |
and let  satisfy it. Then
satisfy it. Then
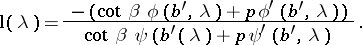 |
If 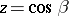 ,
, 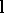 is a meromorphic function in the complex
is a meromorphic function in the complex  -plane; indeed, it is a bilinear transformation. As
-plane; indeed, it is a bilinear transformation. As  varies over real values
varies over real values 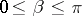 ,
,  varies over the real
varies over the real  -axis, and
-axis, and  describes a circle in the
describes a circle in the  -plane.
-plane.
It can be shown that if  increases, the circles become nested. Hence there is at least one point inside all. For such a point
increases, the circles become nested. Hence there is at least one point inside all. For such a point 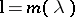 ,
,
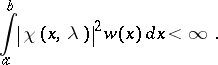 |
There exists at least one solution of 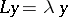 , which is square-integrable.
, which is square-integrable.
If the limit of the circles is a point, then 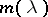 is unique and only
is unique and only 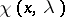 is square-integrable. This is the limit-point case. If the limit of the circles is itself a circle, then
is square-integrable. This is the limit-point case. If the limit of the circles is itself a circle, then 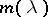 is not unique and all solutions of
is not unique and all solutions of 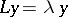 are square-integrable. This is the limit-circle case.
are square-integrable. This is the limit-circle case.
Nonetheless, the differential operator
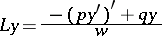 |
whose domain satisfies
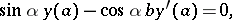 |
 |
where 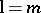 on the limit circle or limit point, is a self-adjoint differential operator (cf. also Self-adjoint operator; Self-adjoint differential equation) on
on the limit circle or limit point, is a self-adjoint differential operator (cf. also Self-adjoint operator; Self-adjoint differential equation) on 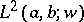 .
.
If the circle limit is a point, the second boundary condition (at 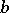 ) is automatic.
) is automatic.
The spectral measure of 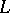 is given by
is given by
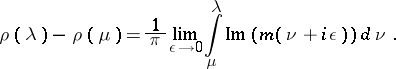 |
The spectral resolution of arbitrary functions in 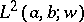 is
is
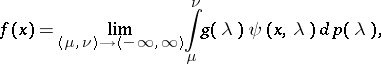 |
where the limit is in the mean-square sense, and
 |
References
| [a1] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) |
| [a2] | A.M. Krall, "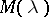 theory for singular Hamiltonian systems with one singular point" SIAM J. Math. Anal. , 20 (1989) pp. 644–700 theory for singular Hamiltonian systems with one singular point" SIAM J. Math. Anal. , 20 (1989) pp. 644–700 |
Titchmarsh-Weyl m-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Titchmarsh-Weyl_m-function&oldid=28680