Difference between revisions of "Wishart distribution"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m |
||
| Line 5: | Line 5: | ||
(<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w0980407.png" /> denotes the trace of a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w0980408.png" />), if the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w0980409.png" /> is positive definite, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804010.png" /> in other cases. The Wishart distribution with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804011.png" /> degrees of freedom and with matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804012.png" /> is defined as the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804013.png" />-dimensional distribution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804014.png" /> with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804015.png" />. The sample covariance matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804016.png" />, which is an estimator for the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804017.png" />, has a Wishart distribution. | (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w0980407.png" /> denotes the trace of a matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w0980408.png" />), if the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w0980409.png" /> is positive definite, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804010.png" /> in other cases. The Wishart distribution with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804011.png" /> degrees of freedom and with matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804012.png" /> is defined as the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804013.png" />-dimensional distribution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804014.png" /> with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804015.png" />. The sample covariance matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804016.png" />, which is an estimator for the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804017.png" />, has a Wishart distribution. | ||
| − | The Wishart distribution is a basic distribution in multivariate statistical analysis; it is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804018.png" />-dimensional generalization (in the sense above) of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804019.png" />-dimensional [[ | + | The Wishart distribution is a basic distribution in multivariate statistical analysis; it is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804018.png" />-dimensional generalization (in the sense above) of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804019.png" />-dimensional [[Chi-squared distribution| "chi-squared" distribution]]. |
If the independent random vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804021.png" /> have Wishart distributions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804023.png" />, respectively, then the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804024.png" /> has the Wishart distribution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804025.png" />. | If the independent random vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804021.png" /> have Wishart distributions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804023.png" />, respectively, then the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804024.png" /> has the Wishart distribution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098040/w09804025.png" />. | ||
Revision as of 11:59, 20 October 2012
The joint distribution of the elements from the sample covariance matrix of observations from a multivariate normal distribution. Let the results of observations have a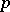 
-dimensional normal distribution 
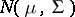with vector mean 
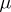and covariance matrix 
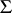. Then the joint density of the elements of the matrix 
is given by the formula
 |
(
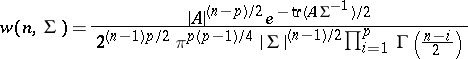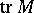denotes the trace of a matrix 
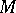), if the matrix 
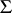is positive definite, and 
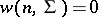in other cases. The Wishart distribution with 
degrees of freedom and with matrix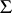 
is defined as the 
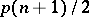-dimensional distribution 
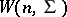with density 
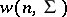. The sample covariance matrix 
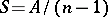, which is an estimator for the matrix 
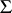, has a Wishart distribution.
The Wishart distribution is a basic distribution in multivariate statistical analysis; it is the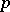 
-dimensional generalization (in the sense above) of the 
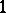-dimensional "chi-squared" distribution.
If the independent random vectors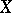 
and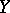 
have Wishart distributions 
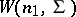and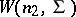 
, respectively, then the vector 
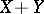has the Wishart distribution 
.
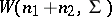The Wishart distribution was first used by J. Wishart [1].
References
| [1] | J. Wishart, Biometrika A , 20 (1928) pp. 32–52 |
| [2] | T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1958) |
Comments
References
| [a1] | A.M. Khirsagar, "Multivariate analysis" , M. Dekker (1972) |
| [a2] | R.J. Muirhead, "Aspects of multivariate statistical theory" , Wiley (1982) |
How to Cite This Entry:
Wishart distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wishart_distribution&oldid=28557
Wishart distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wishart_distribution&oldid=28557
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article