Difference between revisions of "Student distribution"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (dead link removed) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907105.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907105.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907106.png" /> is a random variable subject to the standard normal law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907107.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907108.png" /> is a random variable not depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907109.png" /> and subject to the [[ | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907106.png" /> is a random variable subject to the standard normal law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907107.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907108.png" /> is a random variable not depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907109.png" /> and subject to the [[Chi-squared distribution| "chi-squared" distribution]] with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071010.png" /> degrees of freedom. The distribution function of the random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071011.png" /> is expressed by the formula |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071012.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071012.png" /></td> </tr></table> | ||
Revision as of 11:51, 20 October 2012
with  degrees of freedom,
degrees of freedom, 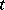 -distribution
-distribution
The probability distribution of the random variable
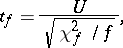 |
where 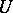 is a random variable subject to the standard normal law
is a random variable subject to the standard normal law 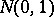 and
and 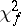 is a random variable not depending on
is a random variable not depending on 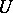 and subject to the "chi-squared" distribution with
and subject to the "chi-squared" distribution with 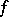 degrees of freedom. The distribution function of the random variable
degrees of freedom. The distribution function of the random variable 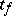 is expressed by the formula
is expressed by the formula
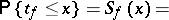 |
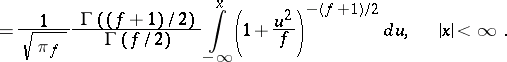 |
In particular, if 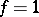 , then
, then
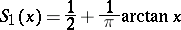 |
is the distribution function of the Cauchy distribution. The probability density of the Student distribution is symmetric about 0, therefore
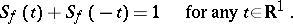 |
The moments 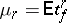 of a Student distribution exist only for
of a Student distribution exist only for 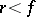 , the odd moments are equal to 0, and, in particular
, the odd moments are equal to 0, and, in particular 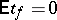 . The even moments of a Student distribution are expressed by the formula
. The even moments of a Student distribution are expressed by the formula
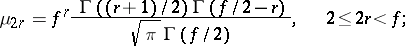 |
in particular, 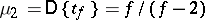 . The distribution function
. The distribution function 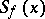 of the random variable
of the random variable 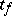 is expressed in terms of the beta-distribution function in the following way:
is expressed in terms of the beta-distribution function in the following way:
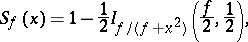 |
where  is the incomplete beta-function,
is the incomplete beta-function, 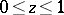 . If
. If 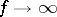 , then the Student distribution converges to the standard normal law, i.e.
, then the Student distribution converges to the standard normal law, i.e.
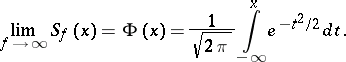 |
Example. Let  be independent, identically, normally
be independent, identically, normally 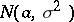 -distributed random variables, where the parameters
-distributed random variables, where the parameters  and
and 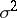 are unknown. Then the statistics
are unknown. Then the statistics
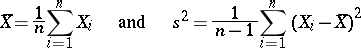 |
are the best unbiased estimators of  and
and 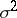 ; here
; here 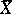 and
and 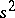 are stochastically independent. Since the random variable
are stochastically independent. Since the random variable  is subject to the standard normal law, while
is subject to the standard normal law, while
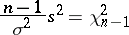 |
is distributed according to the "chi-squared" law with  degrees of freedom, then by virtue of their independence, the fraction
degrees of freedom, then by virtue of their independence, the fraction
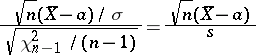 |
is subject to the Student distribution with 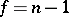 degrees of freedom. Let
degrees of freedom. Let 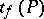 and
and 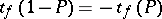 be the solutions of the equations
be the solutions of the equations
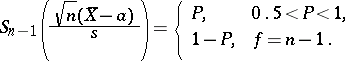 |
Then the statistics 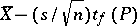 and
and 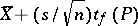 are the lower and upper bounds of the confidence set for the unknown mathematical expectation
are the lower and upper bounds of the confidence set for the unknown mathematical expectation  of the normal law
of the normal law 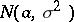 , and the confidence coefficient of this confidence set is equal to
, and the confidence coefficient of this confidence set is equal to 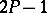 , i.e.
, i.e.
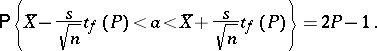 |
The Student distribution was first used by W.S. Gosset (pseudonym Student).
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [3] | "Student" (W.S. Gosset), "The probable error of a mean" Biometrika , 6 (1908) pp. 1–25 |
Student distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Student_distribution&oldid=28550