Difference between revisions of "Vitali theorem"
(→References: Royden: internal link) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Vitali, "Sui gruppi di punti e sulle funzioni di variabili reali" ''Atti Accad. Sci. Torino'' , '''43''' (1908) pp. 75–92</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Vitali, "Sui gruppi di punti e sulle funzioni di variabili reali" ''Atti Accad. Sci. Torino'' , '''43''' (1908) pp. 75–92 {{MR|}} {{ZBL|39.0101.05}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) {{MR|0167578}} {{ZBL|1196.28001}} {{ZBL|0017.30004}} {{ZBL|63.0183.05}} </TD></TR></table> |
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.L. Royden, [[Royden, "Real analysis"|"Real analysis"]], Macmillan (1968) pp. Chapt. 5</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.L. Royden, [[Royden, "Real analysis"|"Real analysis"]], Macmillan (1968) pp. Chapt. 5</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) {{MR|0188387}} {{ZBL|0137.03202}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958) {{MR|0117523}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 {{MR|0257325}} {{ZBL|0176.00801}} </TD></TR></table> |
Vitali's theorem on the uniform convergence of a sequence of holomorphic functions. Let a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678055.png" /> of holomorphic functions on a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678056.png" /> of the complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678057.png" />-plane be uniformly bounded (cf. [[Uniform boundedness|Uniform boundedness]]) and converge on a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678058.png" /> with a limit point in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678059.png" />; the sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678060.png" /> will then converge uniformly inside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678061.png" /> towards a holomorphic function, i.e. will converge uniformly on every compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678062.png" />. The theorem was obtained by G. Vitali . | Vitali's theorem on the uniform convergence of a sequence of holomorphic functions. Let a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678055.png" /> of holomorphic functions on a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678056.png" /> of the complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678057.png" />-plane be uniformly bounded (cf. [[Uniform boundedness|Uniform boundedness]]) and converge on a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678058.png" /> with a limit point in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678059.png" />; the sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678060.png" /> will then converge uniformly inside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678061.png" /> towards a holomorphic function, i.e. will converge uniformly on every compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096780/v09678062.png" />. The theorem was obtained by G. Vitali . | ||
| Line 39: | Line 39: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> G. Vitali, ''Rend. R. Istor. Lombardo (2)'' , '''36''' (1903) pp. 772–774</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> G. Vitali, ''Ann. Mat. Pura Appl. (3)'' , '''10''' (1904) pp. 73</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1''' , Chelsea (1977) pp. Chapt.4 (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P. Montel, "Leçons sur les familles normales de fonctions analytiques et leurs applications" , Gauthier-Villars (1927)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)</TD></TR></table> | + | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> G. Vitali, ''Rend. R. Istor. Lombardo (2)'' , '''36''' (1903) pp. 772–774</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> G. Vitali, ''Ann. Mat. Pura Appl. (3)'' , '''10''' (1904) pp. 73</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1''' , Chelsea (1977) pp. Chapt.4 (Translated from Russian) {{MR|0444912}} {{ZBL|0357.30002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P. Montel, "Leçons sur les familles normales de fonctions analytiques et leurs applications" , Gauthier-Villars (1927) {{MR|}} {{ZBL|53.0303.02}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) {{MR|0180696}} {{ZBL|0141.08601}} </TD></TR></table> |
''E.D. Solomentsev'' | ''E.D. Solomentsev'' | ||
| Line 47: | Line 47: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Carathéodory, "Theory of functions of a complex variable" , '''1''' , Chelsea, reprint (1978) (Translated from German)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.B. Conway, "Functions of one complex variable" , Springer (1973)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Remmert, "Funktionentheorie" , '''II''' , Springer (1991)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Carathéodory, "Theory of functions of a complex variable" , '''1''' , Chelsea, reprint (1978) (Translated from German) {{MR|1570711}} {{MR|0064861}} {{MR|0060009}} {{ZBL|0056.06703}} {{ZBL|0055.30301}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.B. Conway, "Functions of one complex variable" , Springer (1973) {{MR|0447532}} {{ZBL|0277.30001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Remmert, "Funktionentheorie" , '''II''' , Springer (1991) {{MR|1150243}} {{ZBL|0748.30002}} </TD></TR></table> |
Revision as of 12:13, 27 September 2012
Vitali's covering theorem. If a system of closed sets  is a Vitali covering (see below) of a set
is a Vitali covering (see below) of a set 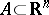 , it is possible to extract from
, it is possible to extract from 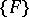 an at most countable sequence of pairwise disjoint sets
an at most countable sequence of pairwise disjoint sets 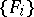 ,
, 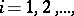 such that
such that
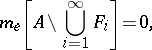 |
where 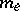 is the outer Lebesgue measure in
is the outer Lebesgue measure in 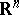 .
.
A Vitali covering of a set 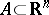 is a system
is a system 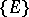 of subsets of
of subsets of 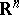 such that for any
such that for any 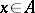 there exists a sequence
there exists a sequence  from
from 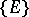 satisfying the following conditions:
satisfying the following conditions:
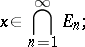 | (1) |
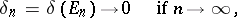 | (2) |
where 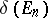 is the diameter of
is the diameter of 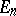 ; and
; and
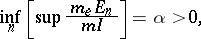 | (3) |
where the supremum is taken over all 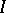 (cubes with faces parallel to the coordinate planes and containing
(cubes with faces parallel to the coordinate planes and containing 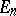 ), and where
), and where 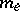 is the outer Lebesgue measure in
is the outer Lebesgue measure in 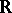 ; this supremum is said to be the regularity parameter of
; this supremum is said to be the regularity parameter of 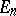 .
.
The theorem was demonstrated by G. Vitali [1] for the case when 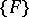 consists of cubes with faces parallel to the coordinate planes. Vitali's theorem is valid as stated if
consists of cubes with faces parallel to the coordinate planes. Vitali's theorem is valid as stated if 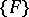 is a Vitali covering of the set
is a Vitali covering of the set 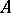 and not for a covering in the ordinary sense. This condition must always be satisfied, even if
and not for a covering in the ordinary sense. This condition must always be satisfied, even if 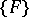 is a system of segments and if to each
is a system of segments and if to each 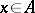 there corresponds a sequence
there corresponds a sequence 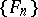 from
from 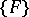 with centres at
with centres at  and with diameters tending to zero.
and with diameters tending to zero.
References
| [1] | G. Vitali, "Sui gruppi di punti e sulle funzioni di variabili reali" Atti Accad. Sci. Torino , 43 (1908) pp. 75–92 Zbl 39.0101.05 |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) MR0167578 Zbl 1196.28001 Zbl 0017.30004 Zbl 63.0183.05 |
Comments
For 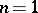 , Vitali's covering theorem is a main ingredient in the proof of the Lebesgue theorem that a monotone function has a finite derivative almost everywhere [a2].
, Vitali's covering theorem is a main ingredient in the proof of the Lebesgue theorem that a monotone function has a finite derivative almost everywhere [a2].
There is another theorem that goes by the name Vitali convergence theorem. Let 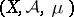 be a measure space,
be a measure space, 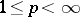 ,
, 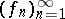 a sequence in
a sequence in 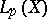 , and
, and 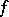 an
an 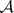 -measurable function which is finite
-measurable function which is finite 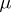 -almost-everywhere and such that
-almost-everywhere and such that 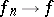
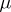 -almost-everywhere. Then
-almost-everywhere. Then 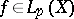 and
and 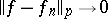 if and only if: 1) for each
if and only if: 1) for each 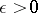 there is a set
there is a set 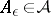 such that
such that 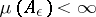 and
and 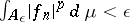 for all
for all 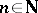 ; and 2)
; and 2) 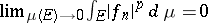 uniformly in
uniformly in  . See [a2].
. See [a2].
At least two other useful theorems bear Vitali's name. The Vitali theorem generalizing the Lebesgue's dominated convergence theorem for what is called an equi-integrable or uniformly integrable family of functions. There is also the Vitali–Hahn–Saks theorem, which asserts that a pointwise limit of a sequence of (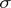 -additive) measures on a
-additive) measures on a 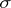 -field is still a (
-field is still a (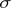 -additive) measure.
-additive) measure.
References
| [a1] | H.L. Royden, "Real analysis", Macmillan (1968) pp. Chapt. 5 |
| [a2] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202 |
| [a3] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523 |
| [a4] | H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 MR0257325 Zbl 0176.00801 |
Vitali's theorem on the uniform convergence of a sequence of holomorphic functions. Let a sequence 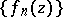 of holomorphic functions on a domain
of holomorphic functions on a domain 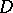 of the complex
of the complex  -plane be uniformly bounded (cf. Uniform boundedness) and converge on a set
-plane be uniformly bounded (cf. Uniform boundedness) and converge on a set 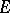 with a limit point in
with a limit point in 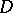 ; the sequence
; the sequence 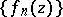 will then converge uniformly inside
will then converge uniformly inside 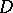 towards a holomorphic function, i.e. will converge uniformly on every compact set
towards a holomorphic function, i.e. will converge uniformly on every compact set  . The theorem was obtained by G. Vitali .
. The theorem was obtained by G. Vitali .
The compactness principle makes it possible to strengthen Vitali's theorem by replacing the condition of uniform boundedness on 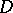 by the condition of uniform boundedness on every compact set
by the condition of uniform boundedness on every compact set 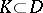 . There also exist Vitali theorems for normal families (cf. Normal family) of meromorphic functions, for families of quasi-analytic functions and for families of holomorphic functions of several complex variables; in the last case, however, additional limitations must be imposed on the set
. There also exist Vitali theorems for normal families (cf. Normal family) of meromorphic functions, for families of quasi-analytic functions and for families of holomorphic functions of several complex variables; in the last case, however, additional limitations must be imposed on the set 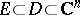 , for example,
, for example, 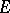 must contain interior points in
must contain interior points in 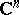 [3], [4].
[3], [4].
References
| [1a] | G. Vitali, Rend. R. Istor. Lombardo (2) , 36 (1903) pp. 772–774 |
| [1b] | G. Vitali, Ann. Mat. Pura Appl. (3) , 10 (1904) pp. 73 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) pp. Chapt.4 (Translated from Russian) MR0444912 Zbl 0357.30002 |
| [3] | P. Montel, "Leçons sur les familles normales de fonctions analytiques et leurs applications" , Gauthier-Villars (1927) Zbl 53.0303.02 |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) MR0180696 Zbl 0141.08601 |
E.D. Solomentsev
Comments
References
| [a1] | C. Carathéodory, "Theory of functions of a complex variable" , 1 , Chelsea, reprint (1978) (Translated from German) MR1570711 MR0064861 MR0060009 Zbl 0056.06703 Zbl 0055.30301 |
| [a2] | J.B. Conway, "Functions of one complex variable" , Springer (1973) MR0447532 Zbl 0277.30001 |
| [a3] | R. Remmert, "Funktionentheorie" , II , Springer (1991) MR1150243 Zbl 0748.30002 |
Vitali theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vitali_theorem&oldid=28282