Difference between revisions of "Stokes formula"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 23: | Line 23: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Spivak, "Calculus on manifolds" , Benjamin (1965)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C. deWitt-Morette, "Analysis, manifolds, physics" , North-Holland (1977) pp. 205 (Translated from French)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Triebel, "Analysis and mathematical physics" , Reidel (1986) pp. 375</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) {{MR|}} {{ZBL|0692.70003}} {{ZBL|0572.70001}} {{ZBL|0647.70001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Spivak, "Calculus on manifolds" , Benjamin (1965) {{MR|0209411}} {{ZBL|0141.05403}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C. deWitt-Morette, "Analysis, manifolds, physics" , North-Holland (1977) pp. 205 (Translated from French) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Triebel, "Analysis and mathematical physics" , Reidel (1986) pp. 375 {{MR|0914975}} {{MR|0880867}} {{ZBL|0607.46047}} </TD></TR></table> |
Revision as of 12:13, 27 September 2012
A formula that expresses the connection between the flow of a vector field through a two-dimensional oriented manifold and the circulation of this field along the correspondingly oriented boundary of this manifold. Let 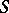 be an oriented piecewise-smooth surface, let
be an oriented piecewise-smooth surface, let 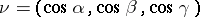 be the unit normal to
be the unit normal to  (at those points, of course, where it exists), which defines the orientation of
(at those points, of course, where it exists), which defines the orientation of 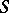 , and let the boundary of
, and let the boundary of 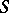 consist of a finite number of piecewise-smooth contours. The boundary of
consist of a finite number of piecewise-smooth contours. The boundary of 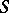 is denoted by
is denoted by 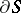 , and is oriented by means of the unit tangent vector
, and is oriented by means of the unit tangent vector  , such that the orientation of
, such that the orientation of 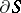 obtained is compatible with the orientation
obtained is compatible with the orientation  of
of 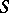 .
.
If 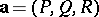 is a continuously-differentiable vector field in a neighbourhood of
is a continuously-differentiable vector field in a neighbourhood of 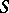 , then
, then
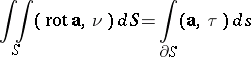 | (*) |
( is the area element of
is the area element of 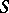 ,
, 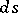 is the differential of the arc length of the boundary
is the differential of the arc length of the boundary 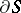 of
of 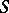 ) or, in coordinate form,
) or, in coordinate form,
 |
Stated by G. Stokes (1854).
Stokes' formula is also the name given to a generalization of formula , which represents the equality between the integral of the exterior differential of a differential form 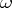 over an oriented compact manifold
over an oriented compact manifold 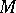 and the integral of the form
and the integral of the form  itself along the boundary
itself along the boundary  of
of 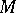 (the orientation of
(the orientation of 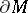 is taken to be compatible with that of
is taken to be compatible with that of 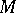 ):
):
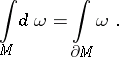 |
Other particular cases of this formula are the Newton–Leibniz formula, the Green formulas and the Ostrogradski formula.
Comments
References
| [a1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) Zbl 0692.70003 Zbl 0572.70001 Zbl 0647.70001 |
| [a2] | M. Spivak, "Calculus on manifolds" , Benjamin (1965) MR0209411 Zbl 0141.05403 |
| [a3] | C. deWitt-Morette, "Analysis, manifolds, physics" , North-Holland (1977) pp. 205 (Translated from French) |
| [a4] | H. Triebel, "Analysis and mathematical physics" , Reidel (1986) pp. 375 MR0914975 MR0880867 Zbl 0607.46047 |
Stokes formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stokes_formula&oldid=28270