Difference between revisions of "Schauder theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Schauder, "Der Fixpunktsatz in Funktionalräumen" ''Stud. Math.'' , '''2''' (1930) pp. 171–180</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Schauder, "Der Fixpunktsatz in Funktionalräumen" ''Stud. Math.'' , '''2''' (1930) pp. 171–180 {{MR|}} {{ZBL|56.0355.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian) {{MR|0539144}} {{MR|0048693}} {{ZBL|0141.11601}} {{ZBL|0096.07802}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958) {{MR|0117523}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) {{MR|0221256}} {{ZBL|0182.16101}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974) {{MR|0488102}} {{ZBL|0286.47037}} </TD></TR></table> |
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Dugundji, A. Granas, "Fixed-point theory" , '''I''' , PWN (1982)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.N. [A.N. Tikhonov] Tychonoff, "Ein Fixpunktsatz" ''Math. Ann.'' , '''111''' (1935) pp. 767–776</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> V.I. Istrăţescu, "Fixed point theory" , Reidel (1981)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. Ryll-Nardzewski, "On fixed points of semi-groups of endomorphisms of linear spaces" , ''Proc. 5-th Berkeley Symp. Probab. Math. Stat.'' , '''2: 1''' , Univ. California Press (1967) pp. 55–61</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Dugundji, A. Granas, "Fixed-point theory" , '''I''' , PWN (1982) {{MR|0660439}} {{ZBL|0483.47038}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.N. [A.N. Tikhonov] Tychonoff, "Ein Fixpunktsatz" ''Math. Ann.'' , '''111''' (1935) pp. 767–776 {{MR|1513031}} {{ZBL|0012.30803}} {{ZBL|61.1195.01}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> V.I. Istrăţescu, "Fixed point theory" , Reidel (1981) {{MR|0620639}} {{ZBL|0465.47035}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. Ryll-Nardzewski, "On fixed points of semi-groups of endomorphisms of linear spaces" , ''Proc. 5-th Berkeley Symp. Probab. Math. Stat.'' , '''2: 1''' , Univ. California Press (1967) pp. 55–61 {{MR|}} {{ZBL|}} </TD></TR></table> |
Revision as of 12:12, 27 September 2012
One of the fixed point theorems: If a completely-continuous operator 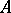 maps a bounded closed convex set
maps a bounded closed convex set 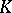 of a Banach space
of a Banach space 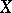 into itself, then there exists at least one point
into itself, then there exists at least one point 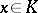 such that
such that 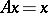 . Proved by J. Schauder [1] as a generalization of the Brouwer theorem.
. Proved by J. Schauder [1] as a generalization of the Brouwer theorem.
There exist different generalizations of Schauder's theorem: the Markov–Kakutani theorem, Tikhonov's principle, etc.
References
| [1] | J. Schauder, "Der Fixpunktsatz in Funktionalräumen" Stud. Math. , 2 (1930) pp. 171–180 Zbl 56.0355.01 |
| [2] | L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian) MR0539144 MR0048693 Zbl 0141.11601 Zbl 0096.07802 |
| [3] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523 |
| [4] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) MR0221256 Zbl 0182.16101 |
| [5] | L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974) MR0488102 Zbl 0286.47037 |
Comments
The Tikhonov fixed-point theorem (also spelled Tychonoff's fixed-point theorem) states the following. Let 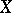 be a locally convex topological space whose topology is defined by a family
be a locally convex topological space whose topology is defined by a family 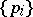 of continuous semi-norms. Let
of continuous semi-norms. Let 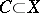 be compact and convex and
be compact and convex and 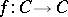 a continuous mapping. Then
a continuous mapping. Then 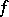 has a fixed point in
has a fixed point in 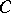 ([a2]; [a3], p. 175). Both the Kakutani fixed-point theorem and the Markov fixed-point theorem are generalized in the Ryll-Nardzewski fixed-point theorem, which states: Let
([a2]; [a3], p. 175). Both the Kakutani fixed-point theorem and the Markov fixed-point theorem are generalized in the Ryll-Nardzewski fixed-point theorem, which states: Let 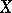 be a Banach space and
be a Banach space and 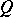 a non-empty weakly compact subset. Let
a non-empty weakly compact subset. Let 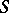 be a semi-group of mappings from
be a semi-group of mappings from 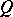 to
to 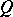 which is non-contracting, then there is a fixed point of
which is non-contracting, then there is a fixed point of 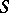 . Here, a family
. Here, a family 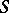 of mappings is said to have a fixed point
of mappings is said to have a fixed point 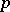 if for every
if for every 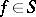 ,
, 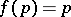 , [a4]; cf. [a3], Chapt. 9, for a discussion of the Ryll-Nardzewski fixed-point theorem in relation to the Kakutani and Markov ones and other fixed-point theorems for families of mappings.
, [a4]; cf. [a3], Chapt. 9, for a discussion of the Ryll-Nardzewski fixed-point theorem in relation to the Kakutani and Markov ones and other fixed-point theorems for families of mappings.
References
| [a1] | J. Dugundji, A. Granas, "Fixed-point theory" , I , PWN (1982) MR0660439 Zbl 0483.47038 |
| [a2] | A.N. [A.N. Tikhonov] Tychonoff, "Ein Fixpunktsatz" Math. Ann. , 111 (1935) pp. 767–776 MR1513031 Zbl 0012.30803 Zbl 61.1195.01 |
| [a3] | V.I. Istrăţescu, "Fixed point theory" , Reidel (1981) MR0620639 Zbl 0465.47035 |
| [a4] | C. Ryll-Nardzewski, "On fixed points of semi-groups of endomorphisms of linear spaces" , Proc. 5-th Berkeley Symp. Probab. Math. Stat. , 2: 1 , Univ. California Press (1967) pp. 55–61 |
Schauder theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schauder_theorem&oldid=28264