Difference between revisions of "Lebesgue measure"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Lebesgue, "Intégrale, longeur, aire" , Univ. Paris (1902) (Thesis)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.R. Halmos, "Measure theory" , v. Nostrand (1950)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , '''1–2''' , Graylock (1957–1961) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Lebesgue, "Intégrale, longeur, aire" , Univ. Paris (1902) (Thesis) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) {{MR|0167578}} {{ZBL|1196.28001}} {{ZBL|0017.30004}} {{ZBL|63.0183.05}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.R. Halmos, "Measure theory" , v. Nostrand (1950) {{MR|0033869}} {{ZBL|0040.16802}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , '''1–2''' , Graylock (1957–1961) (Translated from Russian) {{MR|1025126}} {{MR|0708717}} {{MR|0630899}} {{MR|0435771}} {{MR|0377444}} {{MR|0234241}} {{MR|0215962}} {{MR|0118796}} {{MR|1530727}} {{MR|0118795}} {{MR|0085462}} {{MR|0070045}} {{ZBL|0932.46001}} {{ZBL|0672.46001}} {{ZBL|0501.46001}} {{ZBL|0501.46002}} {{ZBL|0235.46001}} {{ZBL|0103.08801}} </TD></TR></table> |
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) {{MR|0188387}} {{ZBL|0137.03202}} </TD></TR></table> |
Revision as of 12:11, 27 September 2012
in 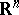
A countably-additive measure 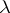 which is an extension of the volume as a function of
which is an extension of the volume as a function of  -dimensional intervals to a wider class
-dimensional intervals to a wider class 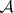 of sets, namely the Lebesgue-measurable sets. The class
of sets, namely the Lebesgue-measurable sets. The class 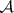 contains the class
contains the class 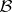 of Borel sets (cf. Borel set) and consists of all sets of the form
of Borel sets (cf. Borel set) and consists of all sets of the form 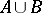 where
where 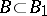 ,
, 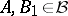 and
and 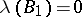 . One has for any
. One has for any 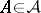 ,
,
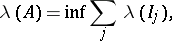 | (*) |
where the infimum is taken over all possible countable families of intervals 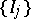 such that
such that 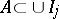 . Formula (*) makes sense for every
. Formula (*) makes sense for every 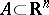 and defines a set function
and defines a set function 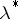 (which coincides with
(which coincides with 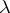 on
on 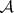 ), called the outer Lebesgue measure. A set
), called the outer Lebesgue measure. A set 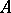 belongs to
belongs to 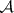 if and only if
if and only if
 |
for every bounded interval 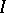 ; for all
; for all 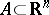 ,
,
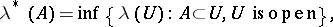 |
and for all 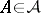 ,
,
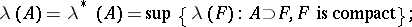 |
if 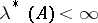 , then the last equality is sufficient for the membership
, then the last equality is sufficient for the membership 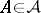 ; if
; if 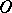 is an orthogonal operator in
is an orthogonal operator in 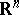 and
and 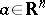 , then
, then 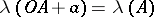 for any
for any 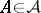 . The Lebesgue measure was introduced by H. Lebesgue [1].
. The Lebesgue measure was introduced by H. Lebesgue [1].
References
| [1] | H. Lebesgue, "Intégrale, longeur, aire" , Univ. Paris (1902) (Thesis) |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) MR0167578 Zbl 1196.28001 Zbl 0017.30004 Zbl 63.0183.05 |
| [3] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
| [4] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801 |
Comments
The Lebesgue measure is a very particular example of a Haar measure, of a product measure (when 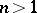 ) and of a Hausdorff measure. Actually it is historically the first example of such measures.
) and of a Hausdorff measure. Actually it is historically the first example of such measures.
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202 |
Lebesgue measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_measure&oldid=28231