Difference between revisions of "Korn inequality"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Fichera, "Existence theorems in elasticity theory" , ''Handbuch der Physik'' , '''VIa/2''' , Springer (1972) pp. 347–389</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Fichera, "Existence theorems in elasticity theory" , ''Handbuch der Physik'' , '''VIa/2''' , Springer (1972) pp. 347–389 {{MR|}} {{ZBL|}} </TD></TR></table> |
Revision as of 12:11, 27 September 2012
An inequality for vector functions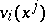 
, 
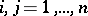, and their derivatives, defined in some bounded domain 
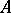of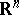 
:
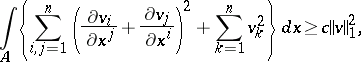 | (1) |
where
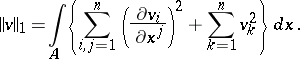 | (2) |
The Korn inequality is also valid for vector functions in the space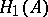 
obtained by completing the space 
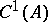with respect to the norm (2). The inequality (1) is sometimes called the second Korn inequality; the first Korn inequality being inequality (1) without the second term on the left.
The inequality was proposed by A. Korn (1908) in order to obtain an a priori estimate for the solution of non-homogeneous equations of elasticity theory.
References
| [1] | G. Fichera, "Existence theorems in elasticity theory" , Handbuch der Physik , VIa/2 , Springer (1972) pp. 347–389 |
How to Cite This Entry:
Korn inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Korn_inequality&oldid=28229
Korn inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Korn_inequality&oldid=28229
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article