Difference between revisions of "Energy of measures"
(Importing text file) |
Greenozavr (talk | contribs) m (corrected mistake) |
||
| Line 1: | Line 1: | ||
A concept in [[Potential theory|potential theory]] that is an analogue of the physical concept of the potential energy of a system of electric charges. For points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035660/e0356601.png" /> of a Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035660/e0356602.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035660/e0356603.png" />, let | A concept in [[Potential theory|potential theory]] that is an analogue of the physical concept of the potential energy of a system of electric charges. For points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035660/e0356601.png" /> of a Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035660/e0356602.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035660/e0356603.png" />, let | ||
| − | + | \[ | |
| + | H(|x|) = \left\{ \begin{array}{rl} | ||
| + | \ln\frac{1}{|x|} & \text{for $n = 2$} \\ | ||
| + | \frac{1}{|x|^{n-2}} & \text{for $n \geq 3$}, | ||
| + | \end{array} \right. | ||
| + | \] | ||
be the fundamental solution of the Laplace equation and let | be the fundamental solution of the Laplace equation and let | ||
Revision as of 13:39, 20 September 2012
A concept in potential theory that is an analogue of the physical concept of the potential energy of a system of electric charges. For points 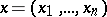 of a Euclidean space
of a Euclidean space 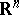 ,
, 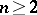 , let
, let
\[ H(|x|) = \left\{ \begin{array}{rl} \ln\frac{1}{|x|} & \text{for '"`UNIQ-MathJax1-QINU`"'} \\ \frac{1}{|x|^{n-2}} & \text{for '"`UNIQ-MathJax2-QINU`"'}, \end{array} \right. \]
be the fundamental solution of the Laplace equation and let
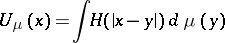 | (2) |
be the Newton (for 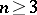 ) or logarithmic (for
) or logarithmic (for 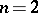 ) potential of a Borel measure
) potential of a Borel measure  on
on 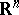 .
.
Restricting from now on to the case 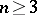 , one defines the mutual energy of two non-negative measures
, one defines the mutual energy of two non-negative measures 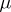 and
and  by
by
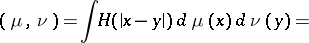 | (3) |
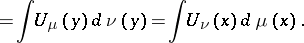 |
Now 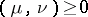 , but it can happen that
, but it can happen that  . The energy of the measure
. The energy of the measure 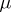 is the number
is the number 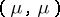 ,
, 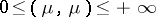 . For two measures
. For two measures 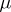 ,
,  of arbitrary sign one can use the canonical decomposition
of arbitrary sign one can use the canonical decomposition 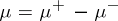 ,
, 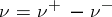 (or any decomposition of the form
(or any decomposition of the form 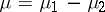 ,
, 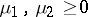 ) and, provided these four measures have finite energy, define the mutual energy of
) and, provided these four measures have finite energy, define the mutual energy of 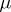 and
and  by
by
 |
which may turn out to be negative, but
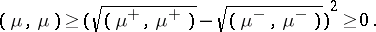 |
The totality 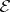 of all measures with finite energy can be made into a pre-Hilbert vector space with the scalar product
of all measures with finite energy can be made into a pre-Hilbert vector space with the scalar product 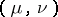 and the energy norm
and the energy norm 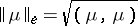 . Here the Bunyakovskii–Cauchy–Schwarz inequality
. Here the Bunyakovskii–Cauchy–Schwarz inequality 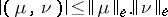 holds as well as the energy principle: If
holds as well as the energy principle: If 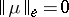 , then
, then 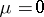 . H. Cartan has shown that the space
. H. Cartan has shown that the space 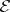 is not complete, but the set
is not complete, but the set 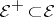 of non-negative measures is complete in
of non-negative measures is complete in  .
.
Let 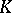 be a compact set in
be a compact set in 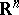 ,
, 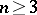 . Among all probability measures
. Among all probability measures 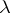 on
on 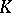 (that is, those for which
(that is, those for which 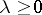 ,
, 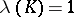 ) there is an extremal capacitary measure
) there is an extremal capacitary measure 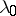 with minimal energy
with minimal energy 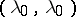 , which is connected with the capacity
, which is connected with the capacity 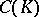 of
of 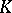 by the relation
by the relation
 | (4) |
If the potential 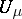 of a measure
of a measure 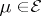 has a square-summable gradient, then
has a square-summable gradient, then
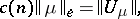 | (5) |
where
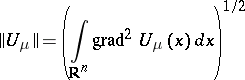 |
is the Dirichlet norm and 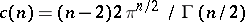 ,
, 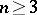 . In fact, (5) remains valid for any measure
. In fact, (5) remains valid for any measure 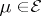 , and the Dirichlet norm
, and the Dirichlet norm 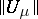 can be defined by an appropriate limit transition.
can be defined by an appropriate limit transition.
In the case of the plane 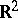 , a direct application of (3) with the logarithmic potential (2) for the definition of the energy of measures is not possible because of the singular behaviour of the logarithmic kernel (1) at infinity. Let
, a direct application of (3) with the logarithmic potential (2) for the definition of the energy of measures is not possible because of the singular behaviour of the logarithmic kernel (1) at infinity. Let  be a bounded domain in
be a bounded domain in 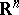 ,
, 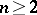 , admitting a Green function
, admitting a Green function 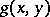 , and let
, and let 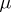 be a Borel measure on
be a Borel measure on  . When one applies Green potentials
. When one applies Green potentials 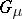 and
and  of the form
of the form
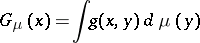 |
instead of Newton potentials 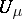 and
and 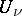 in (3), one obtains for
in (3), one obtains for 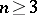 a definition of the energy of measures on
a definition of the energy of measures on  that is equivalent to the one given above, but which turns out to be suitable also for
that is equivalent to the one given above, but which turns out to be suitable also for 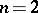 , with preservation of all properties described above (and
, with preservation of all properties described above (and 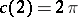 ).
).
References
| [1] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
| [2] | J. Wermer, "Potential theory" , Lect. notes in math. , 408 , Springer (1974) |
| [3] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
Energy of measures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Energy_of_measures&oldid=28050